Classification supervisée, suite (éléments de correction)
Après l'introduction aux arbres de décision réalisée dans le TP précédent, nous allons poursuivre sur ce thème. On va commencer par étudier comment améliorer la performance des arbres de décision induits sur un jeu de données. Ensuite, on verra comment traiter les attributs nominaux.
À l'issue de ce TP, vous m'envoyez par email un compte-rendu (format odt ou pdf) indiquant la réponse aux questions qui sont posées. Vous m'envoyez également un fichier python réalisant toutes les manipulations de ce TP : je dois pouvoir exécuter ce fichier en tapant python3 nom-de-votre-fichier.py et reproduire vos résultats. Cette exécution ne doit pas provoquer d'erreur de python. Remarque : un notebook ne convient pas.
Introduction
On s'intéresse à un jeu de données concernant le diabète. Au début du TP, nous allons utiliser le jeu de données disponible à cet url https://philippe-preux.github.io/ensg/miashs/datasets/pima-made-easy.csv. Comme son nom l'indique, c'est un jeu de données classiques (pima) que j'ai simplifié.
Il y a 9 attributs : 8 sont quantitatifs et le dernier est la classe : patient diabétique (pos) ou pas (neg). Les 8 autres attributs contiennent l'information suivante :
pregnant: nombre de grossesses,glucose: concentration de glucose dans le plasma sanguin 2 heures après un test oral de tolérance au glucose,pressure: pression sanguine diastolique,triceps: épaisseur d'un pli de peau au niveau du triceps,insulin: insuline à 2 heures,mass: IMC,pedigree: pedigré diabétique,age: âge.
À faire : vous chargez ce jeu de données et vous commencez par explorer visuellement ses attributs comme on l'a fait avec les olives. (Visualiser la répartition des valeurs de chaque attribut séparément et visualiser ensuite les données en fonction de chaque paire d'attributs en colorant chaque point en fonction de sa classe.) Voyez-vous quelque chose ? Arrivez-vous à trouver quel attribut pourrait être placé à la racine d'un arbre de décision ?
import numpy as np
graine = int ("ScienceDesDonnees", base=36)%2**31
rs = np.random.RandomState (graine)
####################
# chargement du jeu de données
import pandas as pd
pima = pd.read_csv ("https://philippe-preux.github.io/ensg/miashs/datasets/pima-made-easy.csv")
pima ["diabetes"] = pima ["diabetes"].astype ("category")
import matplotlib.pyplot as plt
pimanumérotés = pima
pimanumérotés ["numéro"] = range (pimanumérotés.shape [0])
attributs = list (pimanumérotés) [0:8]
for attribut in attributs:
pimanumérotés.plot.scatter (x = attribut, y = "numéro", title = "Scatter plot", c = "diabetes", colormap = "plasma")
plt.show ()
del pimanumérotés
Ce qui donne les graphiques suivants :
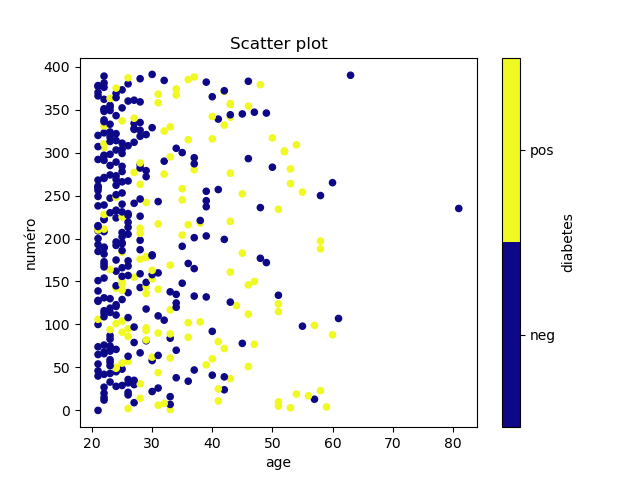
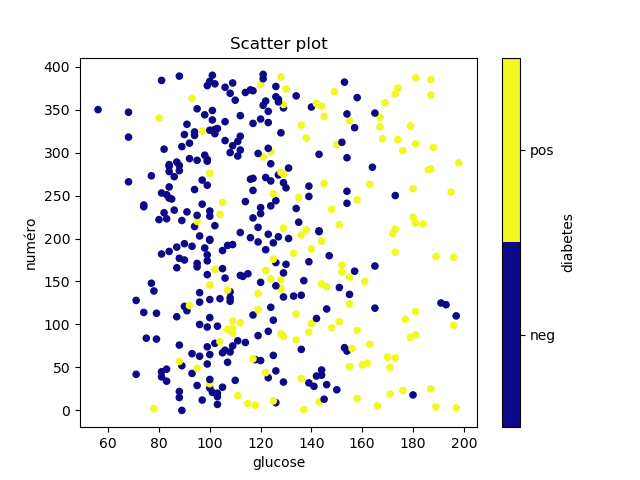
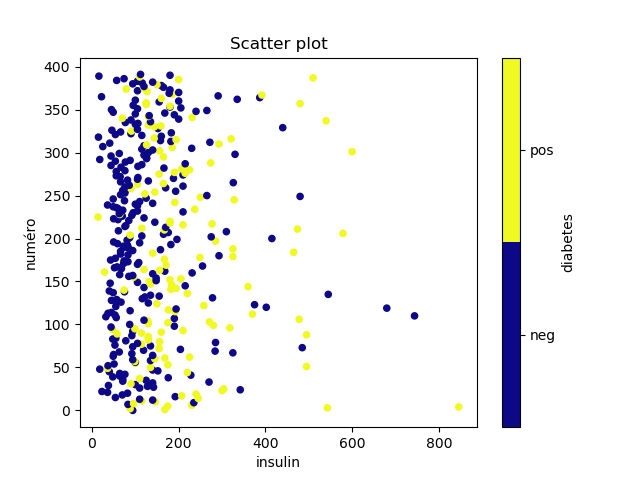
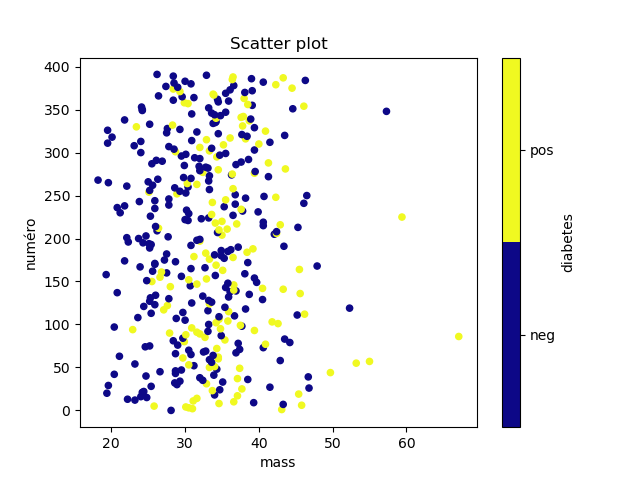
dans lesquels on ne voit pas grand chose. On voit bien que les diabétiques sont plutôt plus âgés, ont plus de sucre dans le sang, etc, mais aucun attribut ne sépare bien les deux classes.
À faire : induire un arbre de décision comme on l'a fait lors du TP précédent. Mesurez son taux de succès sur le jeu de test et son taux de succès moyen et son écart-type dans une validation croisée à 10 plis.
import numpy as np
graine = int ("ScienceDesDonnees", base=36)%2**31
rs = np.random.RandomState (graine)
####################
# chargement du jeu de données
import pandas as pd
pima = pd.read_csv ("https://philippe-preux.github.io/ensg/miashs/datasets/pima-made-easy.csv")
pima ["diabetes"] = pima ["diabetes"].astype ("category")
# induction d'un arbre de décision
from sklearn import tree
from sklearn.model_selection import train_test_split
pimaX_train, pimaX_test, pimaY_train, pimaY_test = train_test_split (pima.iloc [:,:8], pima.diabetes, test_size = .2, random_state = rs)
arbre = tree.DecisionTreeClassifier (random_state = rs)
arbre = arbre.fit (pimaX_train, pimaY_train)
taux_succès = sum (arbre.predict (pimaX_test) == pimaY_test) / pimaX_test. shape [0]
print ("# Le taux de succès de cet arbre mesuré sur le jeu de test est {:.2f}.".format (taux_succès))
# Le taux de succès de cet arbre mesuré sur le jeu de test est 0.72.
'''
# On peut aussi utiliser la méthode score() :
arbre.score (pimaX_test,pimaY_test)
# qui donne le même résultat.
'''
from sklearn.model_selection import cross_val_score
score_cv = cross_val_score (arbre, pima.iloc [:,:8], pima.iloc [:,8], cv = 10)
print ("# Le taux de succès moyen mesuré en validation croisée est {:.2f}., avec un écart-type de {:.2f}". format (np.mean (score_cv), np.std (score_cv)))
# Le taux de succès moyen mesuré en validation croisée est 0.70, avec un écart-type de 0.13.
Influence des paramètres de l'arbre induit
Lors de la création d'un arbre de décision, on dispose de paramètres optionnels qui peuvent être réglés. Ils peuvent avoir un impact important sur le taux d'erreur de l'arbre.
En apprentissage supervisé, il faut toujours garder à l'esprit que le plus gros modèle n'est pas toujours le meilleur. Bien au contraire, très souvent, un modèle moins gros possède un taux d'erreur plus faible. C'est le cas avec les arbres de décision : ce n'est pas le plus grand arbre qui prédit le mieux.
On va étudier trois paramètres :
- le nombre d'exemples minimum associés à une feuille,
- la mesure d'impureté,
- la profondeur de l'arbre.
Nombre d'exemples minimum associés à une feuille
Le paramètre min_samples_leaf de la méthode tree.DecisionTreeClassifier() indique le nombre minimum d'exemples qui sont associés à une feuille lors de l'induction de l'arbre. Par défaut, cette valeur est 1, ce qui est évidemment bien trop petit : avec un seul exemple d'entraînement par feuille, la feuille prédit la classe de cet exemple et cette feuille risque fort de provoquer du sur-apprentissage.
À faire : en suivant la méthodologie vue lors du TP précédent, induire un arbre de décision pour ce jeu de données. (I.e., vous découpez le jeu d'exemples en 80% d'exemples pour l'entraînement, les 20% restants pour le test puis vous induisez l'arbre.)
Ensuite, vous induisez 4 arbres pour lesquels vous spécifiez min_samples_leaf et donnez comme valeur 5, 10, 15, 20.
Vous mesurez l'erreur sur le jeu d'exemples de test de ces 5 arbres. Lequel donne la plus petite erreur ?
Vous effectuez ensuite une validation croisée sur ces 5 arbres et mesurez le taux succès moyen et son écart-type pour chacun. Quel valeur du paramètre produit les arbres réalisant les meilleures prédictions ?
arbre5 = tree.DecisionTreeClassifier (min_samples_leaf = 5, random_state = rs) arbre5 = arbre5.fit (pimaX_train, pimaY_train) arbre10 = tree.DecisionTreeClassifier (min_samples_leaf = 10, random_state = rs) arbre10 = arbre10.fit (pimaX_train, pimaY_train) arbre15 = tree.DecisionTreeClassifier (min_samples_leaf = 15, random_state = rs) arbre15 = arbre15.fit (pimaX_train, pimaY_train) arbre20 = tree.DecisionTreeClassifier (min_samples_leaf = 20, random_state = rs) arbre20 = arbre20.fit (pimaX_train, pimaY_train) taux_succès5 = sum (arbre5.predict (pimaX_test) == pimaY_test) / pimaX_test. shape [0] taux_succès10 = sum (arbre10.predict (pimaX_test) == pimaY_test) / pimaX_test. shape [0] taux_succès15 = sum (arbre15.predict (pimaX_test) == pimaY_test) / pimaX_test. shape [0] taux_succès20 = sum (arbre20.predict (pimaX_test) == pimaY_test) / pimaX_test. shape [0] score_cv5 = cross_val_score (arbre5, pima.iloc [:,:8], pima.iloc [:,8], cv = 10) score_cv10 = cross_val_score (arbre10, pima.iloc [:,:8], pima.iloc [:,8], cv = 10) score_cv15 = cross_val_score (arbre15, pima.iloc [:,:8], pima.iloc [:,8], cv = 10) score_cv20 = cross_val_score (arbre20, pima.iloc [:,:8], pima.iloc [:,8], cv = 10)
J'obtiens les valeurs suivantes :
Valeur de min_samples_leaf | 1 | 5 | 10 | 15 | 20 |
|---|---|---|---|---|---|
| Taux de succès mesuré sur le jeu de test | 0,72 | 0,65 | 0,63 | 0,67 | 0,72 |
| Taux de succès mesuré par valdiation croisée | 0,70 (0,13) | 0,76 (0,09) | 0,77 (0,09) | 0,73 (0,06) | 0,75 (0,08) |
Mesure d'impureté
Comme on l'a vu en cours, on peut mesurer l'impureté (comment les classes sont mélangées dans un jeu d'exemples) de différentes manières, en particulier l'impureté de Gini et l'entropie. Le paramètre criterion de la méthode tree.DecisionTreeClassifier() indique la mesure d'impureté à utiliser lors de l'induction. Par défaut, c'est l'impureté de Gini. Pour utiliser l'entropie, on indique criterion="entropy".
À faire : pour les 5 arbres construits précédemment, vous construisez 5 autres arbres en utilisant l'entropie. Vous mesurez les mêmes taux d'erreur et de succès et vous comparez. L'un des critères donne-t-il de meilleurs résultats ? Quelle combinaison des deux paramètres que nous venons d'étudier donne les meilleurs résultats ?
criterion = "entropy".
J'obtiens les résultats suivantes :
Valeur de min_samples_leaf | 1 | 5 | 10 | 15 | 20 |
|---|---|---|---|---|---|
| Taux de succès mesuré sur le jeu de test | 0,71 | 0,70 | 0,63 | 0,67 | 0,72 |
| Taux de succès mesuré par valdiation croisée | 0,76 (0,05) | 0,76 (0,05) | 0,76 (0,06) | 0,76 (0,05) | 0,77 (0,07) |
En comparant les valeurs contenues dans cette table avec celles de la table précédente, en validation croisée, il semblerait que l'on obtienne de meilleurs résultats avec l'entropie. Pour le taux de succès mesuré sur le jeu de test, cela ne semble pas évident, sauf pour
min_samples_leaf=5.
Profondeur de l'arbre
Le paramètre depth de la méthode tree.DecisionTreeClassifier() indique la profondeur maximale de l'arbre. Ce paramètre permet de limiter la taille de l'arbre.
À faire : en utilisant les meilleurs paramètres trouvés ci-dessus, vous induisez des arbres dont la profondeur varie de 1 à 20. Vous mesurez leur taux d'erreur/taux de succès toujours de la même manière. Vous faites un graphique indiquez cette mesure en fonction de la profondeur. Qu'observez-vous ?
min_samples_leaf=20 et l'entropie.
les_taux_de_succès = [np.nan]
les_taux_de_succès_moyens_par_cv = [np.nan]
les_taux_de_succès_std_par_cv = [np.nan]
for depth in range (1, 20):
arbre_d = tree.DecisionTreeClassifier (min_samples_leaf = 20, criterion = "entropy", max_depth = depth, random_state = rs)
arbre_d = arbre_d.fit (pimaX_train, pimaY_train)
les_taux_de_succès. append (sum (arbre_d.predict (pimaX_test) == pimaY_test) / pimaX_test. shape [0])
score_cv_d = cross_val_score (arbre_d, pima.iloc [:,:8], pima.iloc [:,8], cv = 10)
les_taux_de_succès_moyens_par_cv. append (np.mean (score_cv_d))
les_taux_de_succès_std_par_cv. append (np.std (score_cv_d))
J'obtiens ce graphique montrant le taux de succès en fonction de la profondeur de l'arbre induit mesuré sur le jeu de test et en validation croisée :
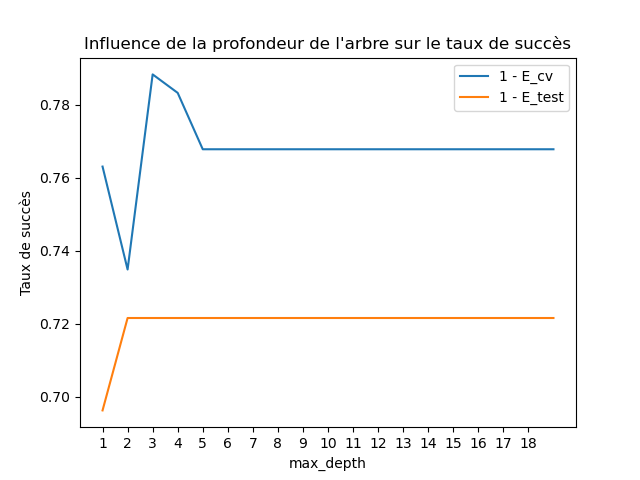
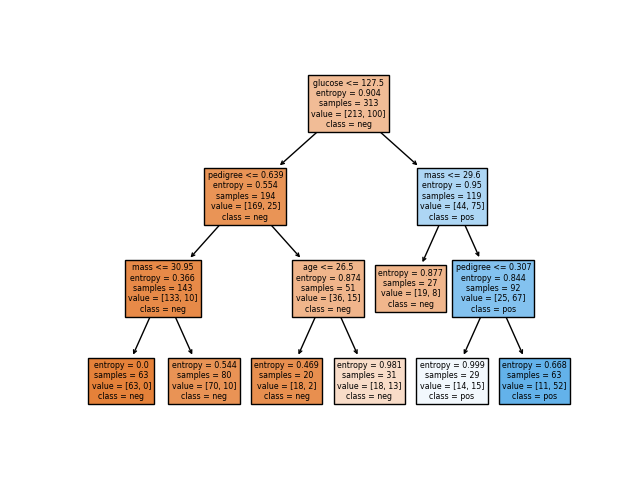
Il semble que le meilleur arbre ait une profondeur de 3 :
Attributs nominaux (ou catégoriques)
Les attributs nominaux sont faciles à traiter pour induire un arbre de décision mais malheureusement, scikit_learn ne sait pas le faire. Il faut utiliser des moyens détournés pour arriver à les prendre en compte, quoique de manière pas très satisfaisante. Comme c'est l'outil que l'on utilise, on va quand même voir comment faire avec cet outil. Mais je ne peux que vous encouragez à ne pas utiliser cette approche et à vous tourner vers un logiciel sérieux : R (ou encore c4.5). Malheureusement, nous n'avons pas le temps d'apprendre à utiliser R dans les quelques heures que dure ce module.
Principe de traitement des attributs nominaux
Nous allons illustrer le principe sur un jeu de données contenant des attrbuts nminaux et des attributs quantitatifs. Ce jeu de données est disponible à cette url https://philippe-preux.github.io/ensg/miashs/datasets/enoughTip.csv. Je suppose par la suite que vous avez chargé ce jeu de données dans un objet dénommé tips.
Aux États-Unis (et dans d'autres pays), à moins d'être un goujat ou d'avoir été particulièrement mal traité par le serveur, on donne systématiquement un pourboire au restaurant et dans les bars. En effet, le service n'est pas inclus dans la note. En principe, ce pourboire s'élève à au moins 15% de la note.
Chaque ligne de ce jeu de données contient des informations concernant une tablée dans un restaurant :
TOTBILL: le montant de la note,TIP: le montant du pourboire laissé par le client,SEX: le sexe du client ayant payé la note,SMOKER: est-il fumeur ou pas ?DAY: le jour,TIME: déjeuner ou dîner ?SIZE: taille de la tablée,enough: est-ce que le pourboire est ≥ 15% ?
Les attributs TOTBILL, TIP et SIZE sont numériques. Les autres attributs sont nominaux. On veut prédire l'attribut enough.
Considérons le premier d'entre-eux, l'attribut DAY qui vaut sun, sat, fri, ou thurs. Pour pouvoir construire un arbre de décision avec scikit_learn, nous devons le transformer en un attribut numérique. La méthode que l'on va utiliser doit fonctionner quel que soit le nombre de valeurs que peut prendre l'attribut (arité de l'attribut). Cette attribut prenant 4 valeurs différentes, il va être transformé en 4 attributs valant 0 ou 1 : chacun de ces 4 attributs correspond donc à l'une des 4 valeurs possibles de l'attribut et 1 seul de ces 4 nouveaux attributs numériques vaudra 1.
Cela pourrait constituer un petit exercice de programmation, mais pandas dispose d'une fonction qui effectue cette transformation pour nous. Faites : pd.get_dummies(tips.DAY).head(). Cela affiche :
fri sat sun thurs 0 0 0 1 0 1 0 0 1 0 2 0 0 1 0 3 0 0 1 0 4 0 0 1 0
alors que cet attribut vaut :
>>> tips.loc[:,"DAY"].head() 0 sun 1 sun 2 sun 3 sun 4 sun Name: DAY, dtype: object
On voit que la valeur d'origine de l'attribut est transformé en un data frame
pandas composé de 4 colonnes, une colonne par valeur possible.
On peut regarder la fin du data frame
>>> tips.loc[:,"DAY"].tail() 239 sat 240 sat 241 sat 242 sat 243 thurs Name: DAY, dtype: object
qui se transforme en :
>>> pd.get_dummies(tips.DAY).tail()
fri sat sun thurs
239 0 1 0 0
240 0 1 0 0
241 0 1 0 0
242 0 1 0 0
243 0 0 0 1
Maintenant que l'on sait transformer un attribut en un ensemble d'attributs numériques, il suffit d'ajouter ces 4 attributs au data frame et de retirer l'attribut nominal d'origine. Pour ajouter les colonnes, on utilise la méthode join() de pandas. Pour retirer une colonne, on utilise la méthode drop () de pandas. Cela s'utilise de la manière suivante :
>>> tips = tips.join (pd.get_dummies(tips.DAY)) tips.drop (columns = ["DAY"], inplace=True)
À faire : faites ce que je viens d'expliquer et traitez de la même manière les autres attributs nominaux (SEX, SMOKER, TIME).
Remarquez que vous pouvez retirer plusieurs colonnes en une seule instruction en indiquant leur nom dans le paramètre columns de la méthode drop().
Induction d'un arbre de décision
Le data frame est maintenant utilisable par l'algorithme d'induction d'arbres de décision.
À faire : en suivant la méthode vue précédemment, induire un arbre de décision. Essayez de l'améliorer en modifiant les paramètres de l'arbre.
Valeurs manquantes
À suivre.