Arbres binaires de recherche

Arbre binaire de recherche (ABR)

On va maintenant utiliser des arbres binaires pour réaliser le tri d'un ensemble de données. On va considérer que l'on dispose d'une liste de nombres à trier. On va construire un arbre ayant certaine propriété ; une fois construit adéquatement, la liste des nombres triée sera obtenu en parcourant l'arbre.
Plus précisément, on va écrire une fonction qui ajoute un élément à un arbre, dans une nouvelle feuille de la manière suivante : soit v la valeur à ajouter, on commence le parcours à la racine de l'arbre déjà construit qui est désigné par l'expression « nœud courant » :
L'arbre ainsi construit est un arbre binaire de recherche (ABR).
On reprend la définition de la classe arbre binaire vue au TP précédent. Le fait que l'arbre soit un ABR n'est pas visible dans la définition de la classe. C'est par construction que c'est un ABR. Aussi, l'ajout d'une valeur dans l'arbre doit-il être réalisé pour garantir que l'on respecte bien la propriété des ABR.

Construction de l'arbre

si v est inférieure à l'étiquette du nœud courant,
- si le nœud courant possède un fils gauche, le fils gauche devient le nœud courant et on continue.
- sinon, ajouter un fils gauche au nœud courant dont l'étiquette est v. On a fini.
si v est supérieure à l'étiquette du nœud courant,
- si le nœud courant possède un fils droit, le fils droit devient le nœud courant et on continue.
- sinon, ajouter un fils droit au nœud courant dont l'étiquette est v. On a fini.

écrire cette méthode d'instance ;
Cela peut s'écrire comme cela :

    def ajouteABR (self, v):
        if v == self. etiquette:
            self. decompte = self. decompte + 1
        elif v < self. etiquette:
            if self. fg == None:
                self. fg = Arbre (valeur = v)
            else:
                self. fg. ajouteABR (v)
        else:
            if self. fd == None:
                self. fd = Arbre (valeur = v)
            else:
                self. fd. ajouteABR (v)

def construitABR (liste):
    first = True
    for valeur in liste:
        if first:
            abr = Arbre (valeur = int (valeur))
            first = False
        else:
            abr. ajouteABR (int (valeur))
    return (abr)

(attention à l'indentation : ajouteABR() est une méthode dans la classe Arbre alors que construitABR() est une fonction.)

la tester. On pourra prendre des listes de nombres fournies via les liens suivants :
- 100 nombres, 200 nombres, 300 nombres, 1000 nombres
comme on l'a dit en cours, on utilise le premier nombre pour créer l'arbre (juste une racine) et ensuite on ajoute les nombres en utilisant la méthode que l'on vient d'écrire.

On ajoute les lignes suivantes pour obtenir l'ABR à partir du fichier contenant 100 nombres :

f = open ("100.nombres", "r")
liste = f.readlines()
abr = construitABR (liste)
f.close ()

Parcours de l'ABR

Une fois construit, on parcourt l'arbre en commençant à la racine et en effectuant le traitement récursif suivant en chaque nœud :

si le nœud courant possède un fils gauche, suivre ce fils gauche et recommencer (appel récursif) ;
afficher l'étiquette du nœud courant (qui peut être une feuille) ;
si le nœud courant possède un fils droit, suivre ce fils droit et recommencer (appel récursif).

Avec ces 4 fichiers de données, on obtient les ABR suivant :

Quelques questions de plus sur les ABR

Quelques méthodes d'instance à implanter :

on a supposé que chaque nombre n'apparaît qu'une seule fois dans la liste. Que se passe-t-il si un nombre apparaît plusieurs fois ? Proposez un mécanisme pour que les occurences multiples d'une même valeur soient traitées intelligemment.

Écrire une méthode d'instance qui détermine si un nombre est présent dans un ABR. La méthode renvoie False ou True selon le cas.
Cela peut s'écrire comme cela :

    def presentDansABR (self, v):
        if v == self.etiquette:
            return (True)
        if v < self.etiquette:
            if self.fg != None:
                return (self.fg.presentDansABR (v))
            else:
                return (False)
        elif self.fd != None:
                return (self.fd.presentDansABR (v))
        return (False)

Écrire une méthode d'instance qui vérifie qu'un arbre binaire respecte la propriété d'un ABR. La méthode renvoie False ou True.

Question à résoudre sur le papier, sans utiliser l'ordinateur :

Dessinez les ABR obtenus pour les 3 listes de nombres suivantes :
1. ABR1 : 10, 5, 20, 1, 7, 6, 9, 18, 23, 21
2. ABR2 : 1, 5, 6, 7, 9, 10, 18, 20, 21, 23
3. ABR3 : 23, 21, 20, 18, 10, 9, 7, 6, 5, 1
Quelle est la hauteur d'un ABR si la liste compte N nombres ? Pouvez-vous répondre à cette question telle qu'elle est posée ? Éventuellement, faites quelques hypothèses pour pouvoir y répondre. Vous pouvez aussi vous demander ce qui se passe si les nombres sont déjà triés dans la liste. Et s'ils sont presque triés ?
Quel est le nombre d'opérations à réaliser au maximum, au minimum, en « moyenne » quand on ajoute une nouvelle valeur à un ABR ?

Parcours d'arbres en profondeur d'abord

Il existe différentes manières de parcourir un arbre binaire. 3 manières sont particulièrement utiles et faciles à programmer récursivement. Elles se distinguent par le moment où l'étiquette du nœud est parcourue : avant les fils, après les fils, entre fils gauche et fils droit.

préfixe : nœud courant avant fils gauche puis droit.
infixe : fils gauche puis nœud courant puis fils droit.
suffixe : fils gauche puis droit puis nœud courant.

À quel parcours correspond le parcours d'un ABR pour obtenir la liste des valeurs triée de manière croissante ?

Égalité de deux ABR

On veut tester si deux ABR sont égaux. Cette égalité de deux ABR peut avoir plusieurs sens :

les deux ABRs contiennent la même liste d'étiquettes.
les deux ABRs ont exactement la même structure et les mêmes étiquettes dans les nœuds correspondant.

Écrire une méthode egal (self, o) qui détermine si les deux arbres ont la même structure (sens 2 ci-dessus).

On utilisera la méthode isinstance (o, Arbre) qui renvoie True si l'object o est une instance de la classe Arbre, ou False sinon.
Note : isinstance (...) doit être utilisé systématiquement pour tester la classe des objets passés en paramètre pour être certain que les opérations qui sont faites dans la méthode sont légitimes.

Écrire une méthode memeContenu (self, o) qui détermine si les deux arbres contiennent les mêmes étiquettes (sens 1 ci-dessus).

Encore quelques questions sur les ABR

On dit qu'un arbre est équilibré si la différence de hauteur entre deux feuilles est inférieure ou égale à 1. Écrire une méthode d'instance qui détermine si un ABR est équilibré.
Écrire une méthode d'instance qui retire une valeur d'un ABR. Vous pouvez vous inspirez du contenu de la page arbre binaire de recherche de Wikipedia.
Écrire une méthode d'instance qui retire d'un ABR toutes les valeurs comprises dans un intervalle fixé.
Écrire une méthode d'instance qui fusionne deux ABR.

Parcours d'un arbre en largeur d'abord

On veut parcourir l'ABR par niveau. Par exemple, pour cet ABR

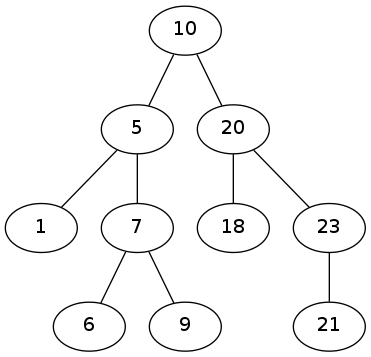
les nœuds sont parcourus dans l'ordre suivant : 10, 5, 20, 1, 7, 18, 23, 6, 9, 21.

Écrire une méthode d'instance qui produit ce parcours.
(Aide : n'essayez pas de le faire de manière récursive.)