Processus aléatoires, statistiques et reproductibilité expérimentale
Ce TP a pour objet de présenter un certain nombre de points liés à la maîtrise de la notion d'aléa dans les expériences informatiques.
Dans les UEs de PDI et APR, nous étudions des algorithmes stochastiques, c'est-à-dire qu'a priori, ils donnent des résultats différents à chacune de leur exécution. Pour étudier le comportement de ces algorithmes, il faut tenir compte de cette variabilité et utiliser les outils adéquats pour cela. Outre la variabilité des résultats, un concept scientifique clé est la capacité à reproduire les résultats d'une expérience. L'objet de ce TP est d'étudier ces notions et d'indiquer comment les prendre en compte concrétement.
Ce TP est réalisé en C ou en python, au choix, pour différentes raisons : 1) contrairement à ce que l'on peut croire, on n'est pas obligé de travailler en Python quand on travaille en apprentissage automatique et ce TP le démontre ; 2) ce TP peut aussi très facilement être réalisé en R par exemple, ou C++ ou bien d'autres langages. Je rappelle que le langage C est le langage le plus vert, le moins consommateur en ressources, le moins pollueur (50x moins que python par exemple). Concrétement, il n'est pas rare qu'un même algorithme codé en C soit 50 voire 100 fois (et même plus) plus rapide que codé en python. Si on doit faire tourner un code lourd, il n'y a pas à hésiter. Par ailleurs, d'une manière générale, un programme en C est bien plus fiable qu'un programme en python.
Génération de nombres pseudo-aléatoires
Pré-requis
On utilise la bibliothèque GSL (GNU Scientific Library) qui contient de multiples fonctions mathématiques. Elle est installée sur les ordinateurs en salle TP. Sur votre ordinateur personnel, il faut peut-être l'installer.
On utilisera le compilateur gcc et on spécifiera les options -lgsl -lgslcblas -lm pour éditer les liens avec les bibliothèques nécessaires dans ce TP.
On utilise la bibliothèque numpy qui doit donc être installée.
Génération de nombres pseudo-aléatoires
Activité 1
La notion de nombres (pseudo-)aléatoires est une notion complexe. La génération d'une séquence de nombres aléatoires par un algoithme est un problème aussi vieux que l'apparition des premiers ordinateurs ; des progrès ont été faits et ils se poursuivent. La fonction de base consiste à générer un entier naturel dont la valeur est comprise entre 0 et 2N-1 où N est le nombre de bits composant les mots manipulés par le(s) microprocesseur(s) pendant un calcul. À chaque appel, cette fonction de base renvoit un nombre différent. On veut que cette séquence de nombres respectent certaines propriétés (par exemple, une distribution uniforme dans l'intervalle de valeurs, ou encore la non répétition de séquences) quel que soit le nombre d'appels à cette fonction, donc quelle que soit la longueur de la séquence de nombres pseudo-aléatoires générés. L'infini n'étant pas atteignable dans un programme d'ordinateur, on veut que ces propriétés soient respectées par des séquences aussi longues que possibles.
Question : combien de séquences d'entiers différentes sont possibles avec un ordinateur travaillant sur N bits ?
Remarque : vous avez noté l'utilisation du mot « pseudo » avant le mot aléatoire. On veut ainsi distinguer un nombre aléatoire au sens mathématique du terme d'un nombre calculé par un algorithme pour donner l'impression que la séquence de nombres est aléatoire. Curieusement, l'algorithme qui calcule une telle séquence est déterministe : la séquence est construite à l'aide d'une (simple) équation de récurrence. Le premier terme (ou les premiers termes) de cette séquence est fourni par l'utilisateur et se nomme la graine.
Quand on exécute un programme utilisant un générateur de nombres pseudo-aléatoires, il faut impérativement sauvegarder la valeur de la graine. C'est le seul moyen de ré-exécuter exactement de la même manière un programme.
Remarque : nous n'abordons pas ce point dans le cadre de ce TP ni de ce cours, mais la génération de nombres pseudo-aléatoires par un programme distribué ou simplement mutli-threadé complique les choses : les différentes séquences de nombres doivent êtres différentes mais elles doivent respecter des propriétés globales.
Autre remarque : d'un point de vue scientifique, on ne sait pas si l'aléatoire existe. Toute la physique, donc l'explication du monde, est déterministe jusqu'à la découverte de la physique quantique au début du XXè siècle. Celle-ci semble s'appuyer sur des processus intrinséquement aléatoires, mais c'est peut-être juste que nous ne l'avons pas encore bien comprise. La physique quantique a profondément perturbé les physiciens et plus généralement les scientifiques dans leur appréhension du monde.
À partir d'un générateur d'entiers pseudo-aléatoires compris entre 0 et le plus grand entier non signé (que je note MAX_INT), on obtient facilement un nombre « réel » (flottant) compris dans [0, 1] en divisant cet entier par MAX_INT. Comme il est très courant d'avoir besoin de générer des nombres dans cet intervalle, il y a généralement une fonction qui le fait directement, c'est-à-dire qui renvoit un nombre pseudo-aléatoire dans l'intervalle [0, 1].
| C | python |
|---|---|
|
En C, on utilise typiquement une fonction qui génère un entier naturel pseudo-aléatoire compris entre 0 et
static gsl_rng *prng = NULL; prng = gsl_rng_alloc (gsl_rng_mt19937);
Il existe de nombreuses manières de générer une séquence de nombres pseudo-aléatoires. Ici on utilise le Mersenne Twister en spécifiant |
En python, on utilise typiquement une fonction de la bibliothèque import numpy as np np.random.rand (1) affiche un nombre pseudo-aléatoire compris entre 0 et 1 (0 inclus, 1 exclus). En procédant ainsi, on utilise un algorithme qui se nomme PCG64 qui est plus récent que le Mersenne Twister et génère de meilleures séquences de nombres pseudo-aléatoires. |
Question 1 : écrire un programme qui affiche une suite de 10 nombres pseudo-aléatoires compris entre 0 et 1.
Activité 2
Exécutez plusieurs fois le programme précédent et comparez les résultats : qu'observez-vous ?
En science, quand on effectue une expérience, il y a un principe fondamentale qui est celui de la reproductibilité : si je fais plusieurs fois la même expérience dans les mêmes conditions, le résultat doit toujours être le même.
En informatique, dans certaines conditions, exécuter un programme est analogue à la réalisation d'une expérience. En appliquant le principe fondamental ci-dessus, on veut qu'exécuter un même programme plusieurs fois donne toujours le même résultat (dans la mesure du possible, ce n'est pas toujours faisable). Et si on veut qu'un programme donne des résultats différents à chaque exécution, on veut que cette variabilité soit contrôlée, c'est-à-dire qu'elle soit elle-même reproductible : on veut que l'aléatoire ce ne soit pas n'importe quoi, mais un aléatoire reproductible.
La solution à ce problème est très simple. Elle consiste à initialiser la série de nombres pseudo-aléatoires avec un certain nombre qui se nomme une graine. Si on fournit une certaine graine à un certain générateur de nombres pseudo-aléatoires, il génère ensuite toujours la même séquence de nombres (puisqu'il est déterministe). Dans les exemples ci-dessous, on utilise la graine 123456. Utilisez celle que vous voulez.
| C | python |
|---|---|
|
En C, à la suite de ce qui a été expliqué plus haut, on fixe la graine par un appel à la fonction |
En python, on crée un générateur de nombres pseudo-aléatoires par |
Question 2 : modifier le programme en initialisant correctement la graine. L'exécuter plusieurs fois. Que constatez-vous ?
Question 2bis : comparer la séquence de nombres (une dizaine) par le programme avec la graine n, n+1 et n-1. Que constatez-vous ? Connaissez-vous un moyen de comparer ces séquences de nombres ?
Activité 3
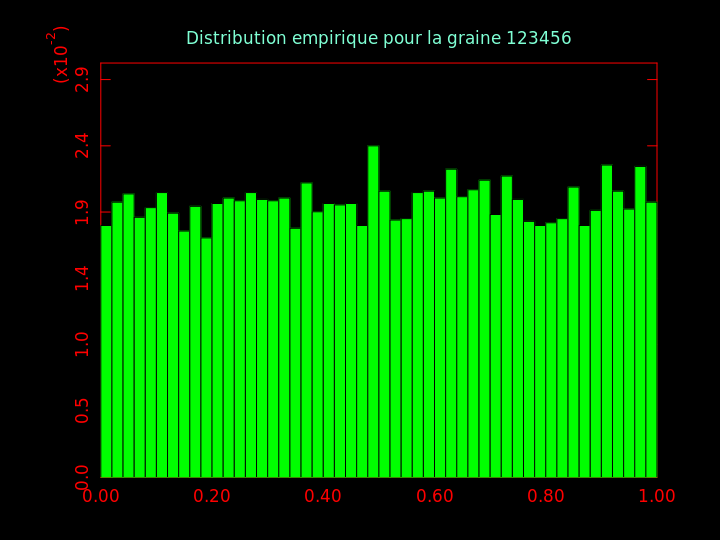
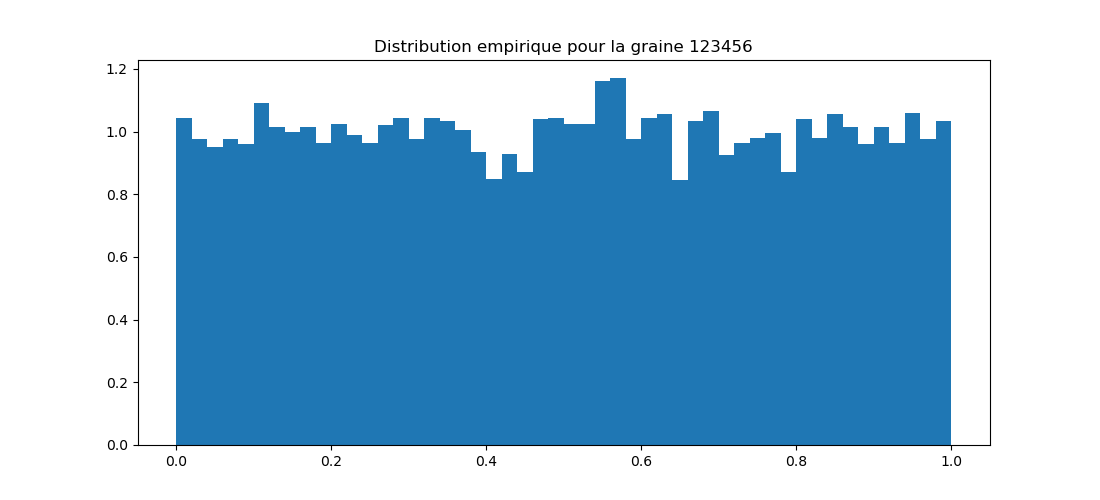
Les nombres générés précédemment sont uniformément répartis dans l'intervalle [0, 1]. On va le vérifier en réalisant un histogramme.
Question 3 : générer 10.000 nombres pseudo-aléatoires compris dans [0, 1] et en faire un histogramme.
| C | python |
|---|---|
|
En C, on va utiliser la bibliothèque PLplot qui permet de réaliser des graphiques. Le but de ce TP n'étant pas d'apprendre à utiliser PLplot, je mets à votre disposition deux fichiers que vous allez utilisez :
Vous pouvez écrire une fonction qui calcule l'histogramme vous-même ou utiliser les fonctions de la GSL qui calculent un histogramme. Puis : barplot (les_valeurs, les_bords, n, titre)
Et on obtient :
|
En python, en plus de ce que l'on a vu pour générer des nombres pseudo-aléatoires, on va obtenir l'histogramme en utilisant la fonction |
Question 3bis : comparer visuellement ces histogrammes ; qu'en pensez-vous ?
Question 3ter : générer les histogrammes pour les graines n, n+1 et n-1. Que constatez-vous ?
Activité 4
Il est courant de vouloir générer des nombres pseudo-aléatoires dont la distribution n'est pas uniforme. Il existe en effet des tas de distributions de probabilités. On distingue les distributions discrètes des distributions continues. Par exemple, si on veut simuler le lancer d'un dé à 6 faces, on génère un nombre dans l'ensemble { 1, 2, 3, 4, 5, 6 } ; si on veut simuler le lancer d'une pièce (pile ou face), on génère 0 ou 1, de manière équi-probable si la pièce est équilibrée, ou avec une probabilité p pour l'un et 1-p pour l'autre si la pièce est déséquilibrée. Dans le premier cas (lancer de dé), c'est une distribution uniforme discrète ; dans le troisième (pièce non équilibrée), c'est une loi de Bernoulli de paramètre p ; le deuxième cas (pièce équilibrée) peut être vu soit comme une loi uniforme, soit comme une loi de Bernoulli avec p=1/2.
Pour de très nombreuses lois de distribution de probabilités, il existe une fonction qui génère des nombres pseudo-aléatoires suivant cette loi. L'une des plus connues est la loi normale (ou gaussienne, ou « en cloche »).
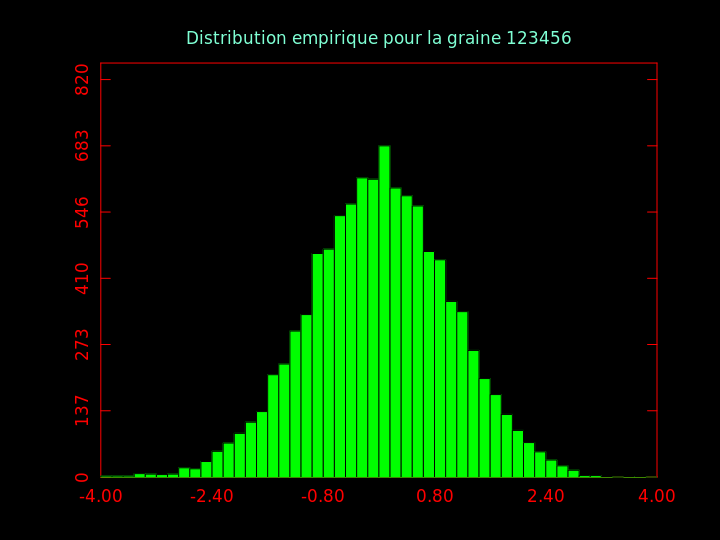
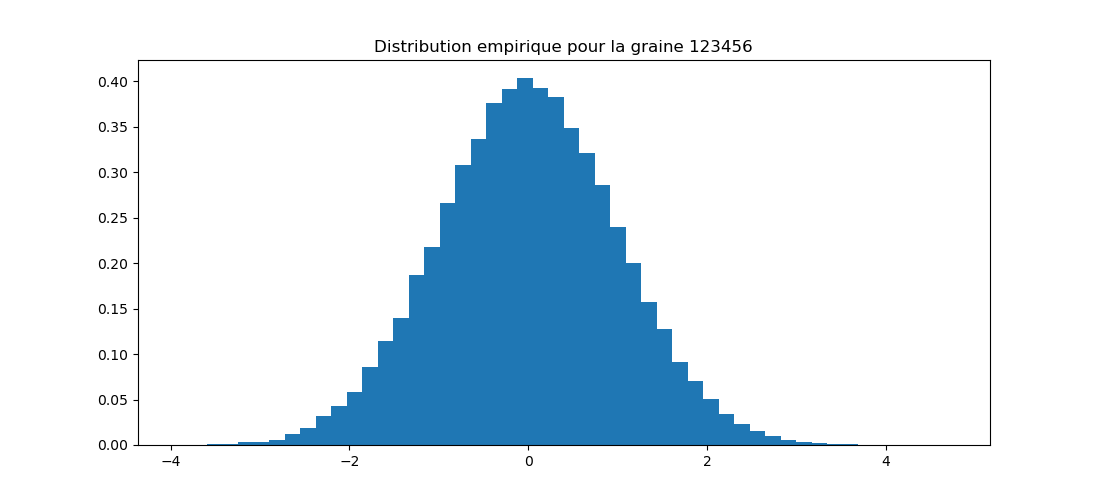
Question 4 : générer 10.000 nombres pseudo-aléatoires distribués normalement (moyenne nulle, écart-type 1) et en faire un histogramme.
| C | python |
|---|---|
|
Avec la GSL, on génère un nombre pseudo-aléatoire selon une loi normale de moyenne nulle et d'écart-type s à l'aide de la fonction |
En python, on génère n nombres pseudo-aléatoires selon une loi normale de moyenne m et d'écart-type s à l'aide de la fonction |
Activité 5
On va maintenant écrire notre propre générateur de nombres pseudo-aléatoires. Même s'il n'aura pas les bonnes propriétés des générateurs vus précédemment, il aura l'avantage d'être simple et de montrer comment on peut générer des nombres pseudo-aléatoires avec un algorithme déterministe.
Ce générateur engendre des nombres compris dans ]0, 1[. Il s'appuie sur une équation de récurrence très simple : xn+1 ← m xn + c [q].
Dans cette équation, m, c et q sont des paramètres entiers.
La notation [q] signifie « reste de la division du terme de gauche (m xn + c) par q ».
Si à un moment xn est nul, il faut le remplacer par c.
La graine correspond à la valeur de x0.
Le nombre pseudo-aléatoire est obtenu en divisant xn+1 par q.
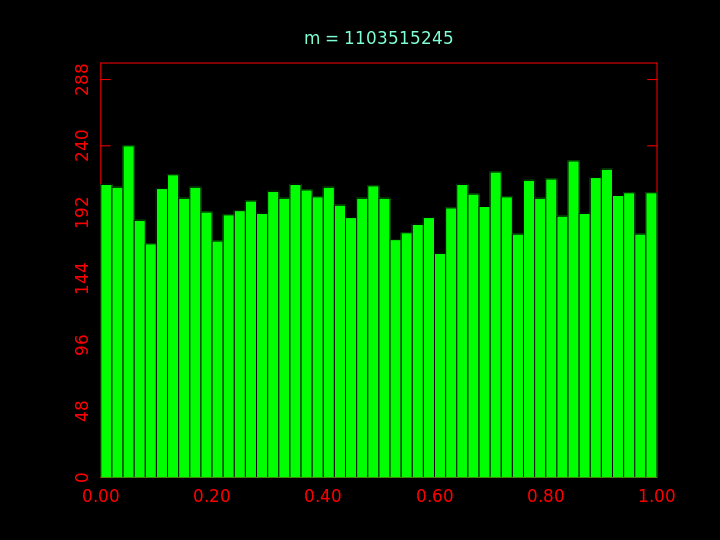
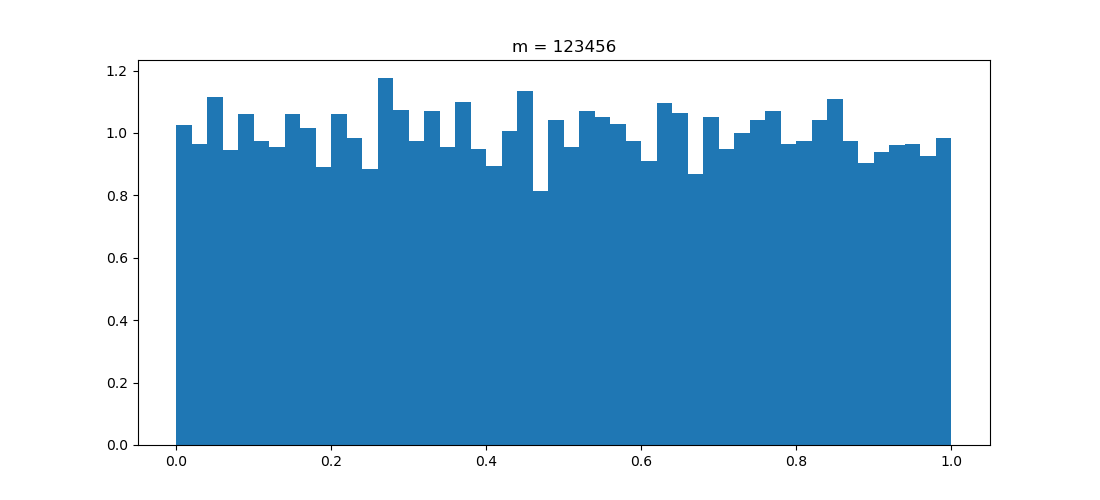
Question 5 : implanter ce générateur de nombres pseudo-aléatoires en prenant m = 1103515245, c = 12345 et q = 231. Générer 10.000 nombres et en faire un histogramme. Le résultat correspond-il à vos attentes ?
J'obtiens ces histogrammes :
Question 5bis : prendre c = 1 et m = 127, générer 10.000 nombres et faites un histogramme. Ensuite, prendre c = 1 et m = 128, générer 10.000 nombres et faites un histogramme. Le résultat correspond-il toujours à vos attentes ?
Activités libres
On indique ici des activités supplémentaires. Vous êtes vivement encouragés à les réaliser.
- En python, pour générer des nombres pseudo-aléatoire avec le Mersenne Twister, il faut utiliser :
from numpy.random import RandomState gnpa = RandomState (seed)
à la place de ce qui a été indiqué plus haut (qui utilise PCG64).
Écrivez les mêmes programmes en C et en python qui chacun génére 10000 nombres pseudo-aléatoires avec le Mersenne Twister. Faites les histogrammes, comparez. Qu'en pensez-vous ? - De même, générer seulement 10 nombres pseudo-aléatoires avec le Mersenne Twister en C et en python. Affichez-les et comparez-les. Que constatez-vous ?
- Python utilise un générateur dénommé PCG64. Celui-ci n'est pas disponible dans la GSL mais son code est disponible sur Internet. Écrire un programme en C qui utilise ce générateur et faites les mêmes comparaisons que ci-dessus avec le Mersenne Twister.
- Et pour finir, un peu de lecture :
- test pour évaluer les qualités d'un générateur de nombres pseudo-aléatoires : dieharder.
- pour en savoir plus sur les nombres pseudo-aléatoires et leur génération : Random Number Generation de L'Ecuyer ; 2è volume de The Art of Computing, Seminumerical Algorithms de D. Knuth ; le chapitre 7 des Numerical recipes in C.
Quelques notions essentielles de statistiques
Face à un processus qui donne des résultats différents, on essaie de résumer ceux-ci sous une forme facile à appréhender et qui caractérise le processus. C'est l'objectif des histogrammes faits précédemment. Plus généralement, un graphique peut décrire de manière simple une séquence de nombres. Il existe des tas de types de graphiques qui permettent de représenter telle ou telle propriété. D'une manière générale, c'est un domaine de recherche complet qui entend rendre intelligible de manière graphique un ensemble de données, la visualisation de données.
Il y a d'autres manières de réaliser un résumé de manière quantitative, issues des statistiques descriptives. La plus connue est la moyenne.
Activité 6
Il est important de connaître la « manière statistique » d'envisager la situation. Celle-ci suppose qu'il existe un processus qui engendre des données (dans ce TP, c'est un algorithme de génération de nombres pseudo-aléatoires), processus dont les propriétés existent mais sont inconnues. Par exemple, on suppose que les nombres générés par ce générateur ont une certaine moyenne, mais on ne la connait pas. Cette moyenne inconnue est nommée la vraie moyenne. Dès lors, on va essayer de la déterminer ; en statistiques, on dit qu'on l'estime.
Question 6 : d'après vous, quelle est la valeur moyenne des nombres générer de manière uniforme dans l'intervalle [0, 1] ? Même question si les nombres sont générés dans [0, 1[ ou dans ]0, 1[ ou dans ]0, 1].
Faites l'expérience suivante : écrire un programme qui engendre 10 nombres pseudo-aléatoires uniformément répartis entre 0 et 1 (comme vu plus haut) et qui affiche la moyenne des i premiers nombres, pour i de 1 à 10.
| C | python |
|---|---|
|
En C, j'obtiens :
0.12697 0.3209415 0.5362003 0.6266815 0.5534404 0.578837 0.6243227 0.6436361 0.6139821 0.6457462 |
En python, j'obtiens :
0.6365137498589308 0.5106627073737531 0.35625694539149694 0.5060058939475681 0.5860149024786793 0.5645073445412173 0.5239396490587402 0.5379657933633322 0.5871596707079398 0.6096868822693744 |
Qu'en pensez-vous ?
Refaire le même genre de chose mais cette fois-ci, générer 106 nombres pseudo-aléatoires et afficher leur moyenne toutes les 105 itérations (la moyenne de tous les nombres qui ont été générés jusqu'à cette itération).
| C | python |
|---|---|
|
En C, j'obtiens : 0.502091 0.50168 0.500681 0.500621 0.500484 0.500331 0.500313 0.500292 0.500307 0.50028 |
En python, j'obtiens : 0.49998361543953534 0.5005033518601376 0.5005979192226971 0.5004579771726371 0.5004691791699108 0.5005069039996045 0.5003719607781464 0.5002382648383843 0.5002204247517089 0.500302828901582 |
Qu'en pensez-vous ? Qu'est-ce qui change ? Pourquoi ?
Vocabulaire :
jusqu'à maintenant, on a utilisé le vocabulaire de l'informatique pour parler de la génération de nombres pseudo-aléatoires. Quand on se met à réflêchir sous l'angle des statistiques et d'un processus qui génère des données, on a l'habitude d'utiliser le vocabulaire des statistiques. Les termes sont synonymes :
au lieu de « générer un nombre pseudo-aléatoire » on dit qu'on « échantillonne » un processus (to sample en anglais),
et au lieu d'un « nombre pseudo-aléatoire » on parle d'« échantillon » (a sample en anglais).
Quand on calcule la moyenne de plusieurs échantillons, on parle de moyenne empirique. Le mot « empirique » signifie ici que l'on calcule la moyenne de valeurs observées/mesurées, engendrées par un processus que l'on observe. Il s'oppose au mot « vrai » introduit plus haut qui signifie que l'on considère la valeur théorique, laquelle n'est pas observée, mais que l'on essaye d'estimer au mieux.
La moyenne est une quantité que l'on peut calculer parmi des tas d'autres, probablement la plus connue. Il existe également la médiane, la variance, l'écart-type et bien d'autres. Chacune de ces quantités se nomme une statistique.
En termes de notation, on a l'habitude de noter la moyenne par la lettre grecque μ et de la distinguer de \( \hat{\mu} \) : sans chapeau, c'est la vraie valeur, avec un chapeau c'est une valeur empirique, ou encore, une estimation de la vraie valeur de la moyenne. Plus généralement, si on note une statistique avec une certaine lettre, on lui ajoute un chapeau quand on veut parler d'une estimation de cette statistique, qui peut être une valeur empirique ; sans chapeau, c'est la vraie valeur de la statistique.
Activité 7
On considère n variables aléatoires indépendantes et identiquement distribuées (i.i.d.) notées Xi de moyenne μ.
La loi des grands nombres indique que la moyenne de ces Xi tend vers μ lorsque n tend vers l'infini.
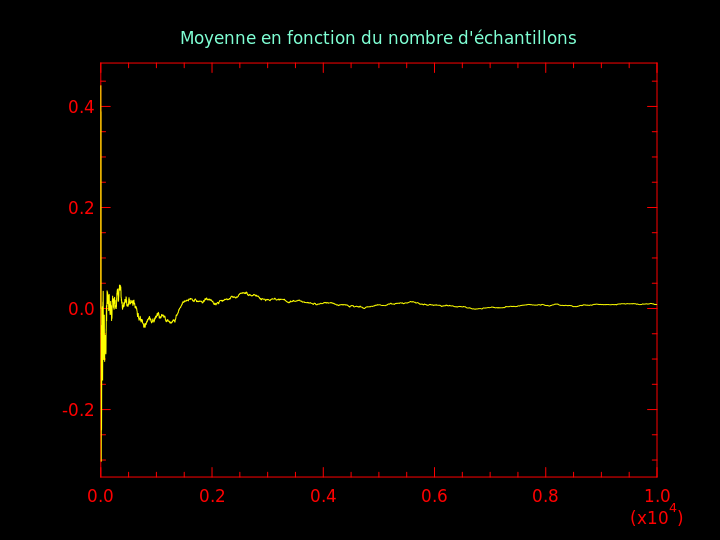
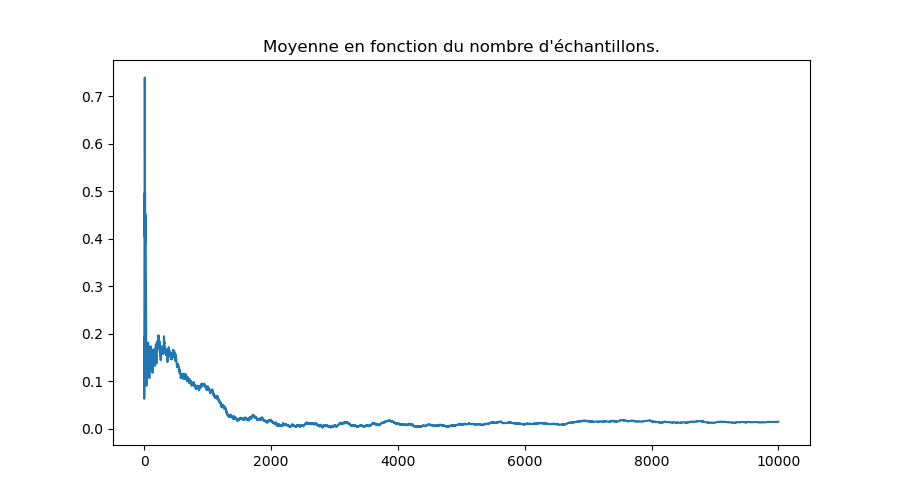
Question 7 : générer 10000 nombres pseudo-aléatoires distribués selon une loi normale de moyenne nulle et d'écart-type 1 (loi que l'on note par la suite \( {\cal N} (0, 1) \)). Calculer la moyenne des i premiers nombres pour i variant de 1 à 10000 et en faire un graphique.
| C | python |
|---|---|
|
En C, le fichier
On obtient cela :
|
En python, on utilise la fonction |
Question 7bis : faire 10 fois la même chose qu'à la question 10 et afficher toutes les moyennes sur un même graphique.
J'obtiens ce qui suit :
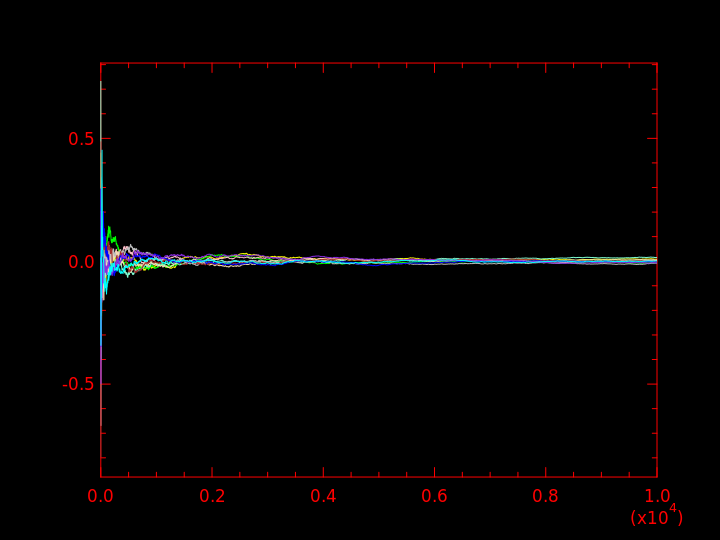
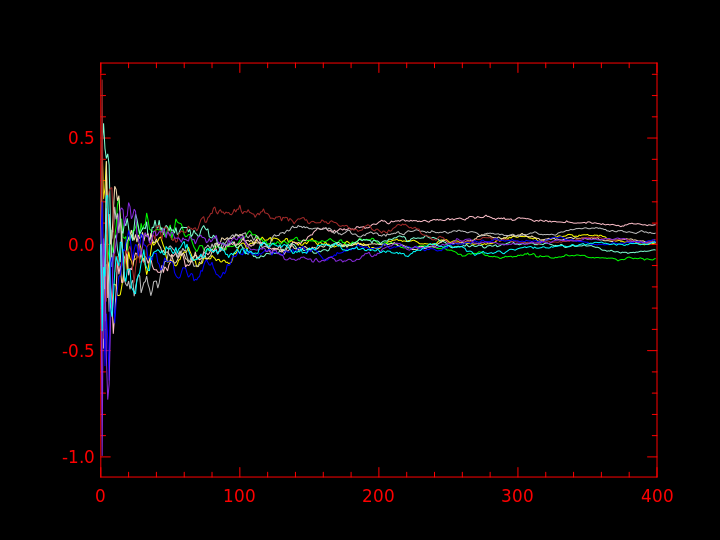
La figure de droite étant juste un agrandissement sur les 400 premières itérations de la figure de gauche.
| C | python |
|---|---|
|
En C vous utilisez la même fonction qu'à la question précédente mais cette fois-ci vous affichez plusieurs tableaux de |
En python, on utilise la fonction |
On voit que la moyenne empirique tend vers 0, qui, par définition, est la vraie moyenne de la distribution \( {\cal N} (0, 1) \).
La vitesse de convergence de la moyenne empirique vers la vraie moyenne est connue : l'écart entre les deux diminue comme \( \frac{1}{\sqrt{i}} \).
On peut l'observer en ajoutant \( \pm \) cette valeur en pointillés sur les graphiques précédents :
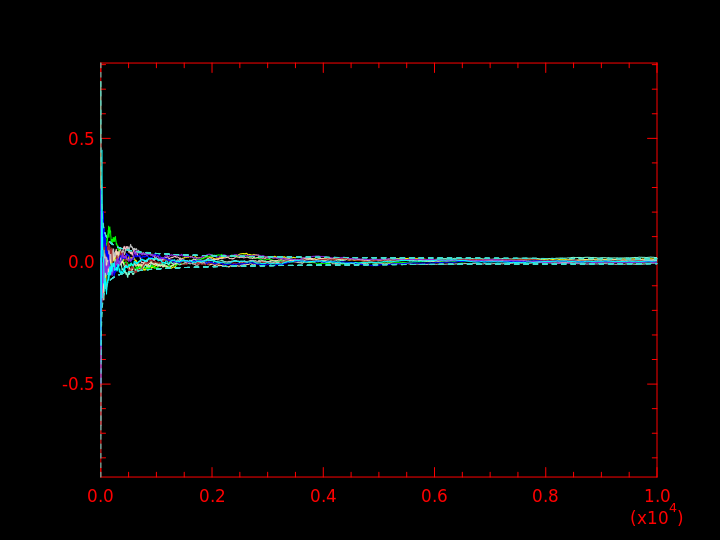
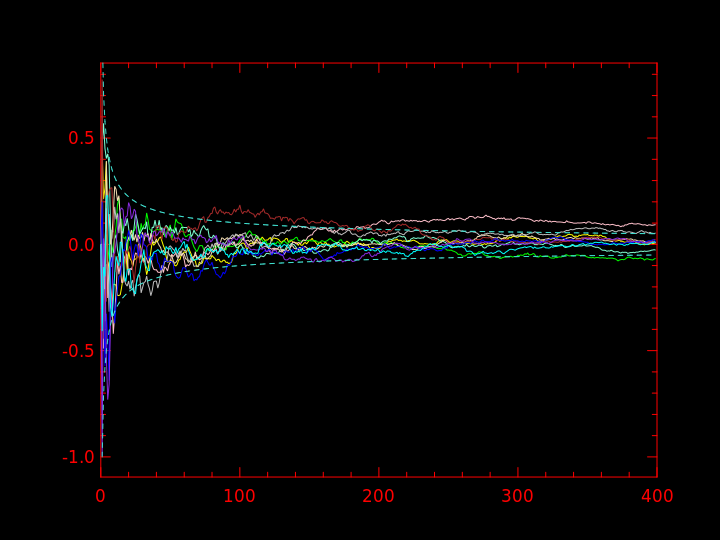
Activité 8
Question 8 : tirer 1000 nombres d'une distribution \( {\cal N} (0, 1) \). En calculer leur moyenne : on obtient une certaine valeur m1. Répéter cette expérience 300000 fois. Nous aurons 300000 valeurs m1 à m300000. En faire un histogramme.
J'obtiens cela :
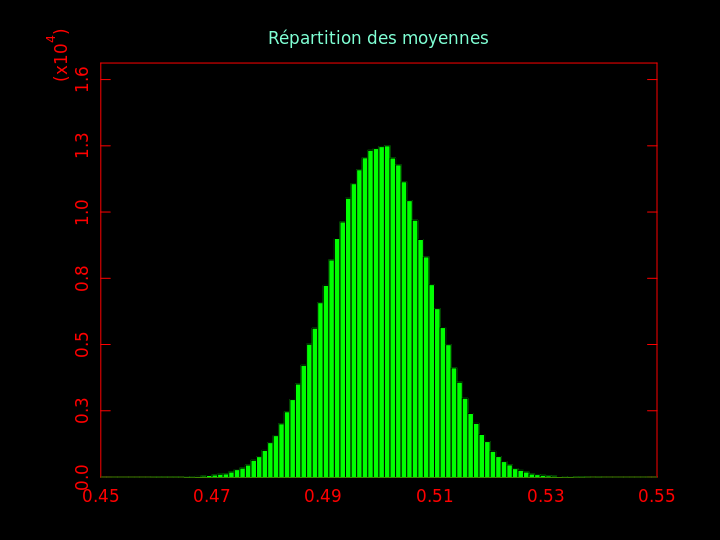
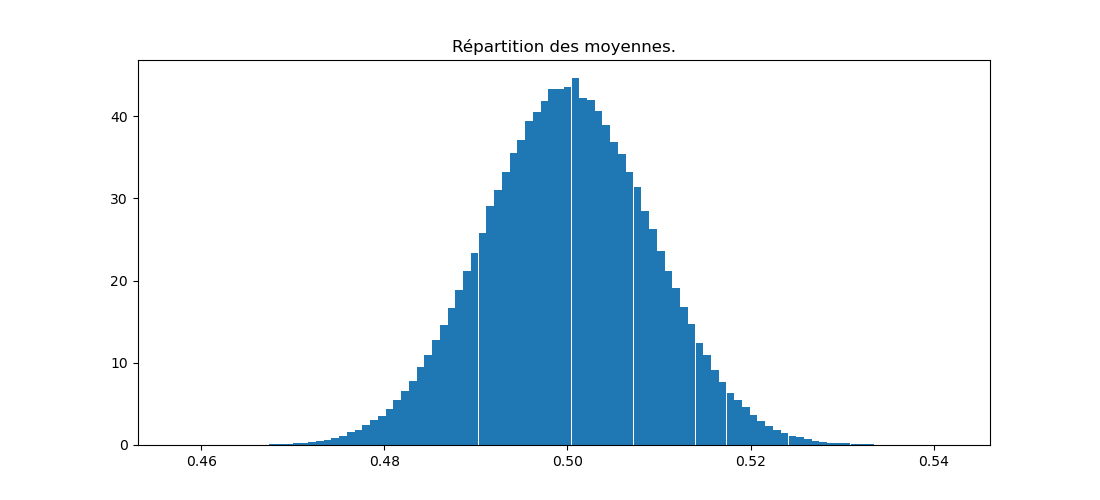
Cela illustre le théorème central limite : chaque mi calculée plus haut est une variable aléatoire.
À chaque itération, chacun des n (= 1000) nombres pseudo-aléatoires a été tiré d'une distribution normale \( {\cal N} (\mu, \sigma) \) avec \( \mu = 0 \) et \( \sigma = 1 \).
Les valeurs de la variable aléatoire m (chacune est la moyenne de 1000 nombres pseudo-aléatoires) sont distribuées selon une loi normale \( {\cal N} (0, \sigma = \frac{1}{\sqrt{n}}) \), soit ici \( {\cal N} (0, \sigma = \frac{1}{\sqrt{1000}}) \), soit environ \( {\cal N} (0, \sigma = 0.03) \).
Pour des nombres distribués uniformément dans [0, 1], on obtient le même genre de graphique :
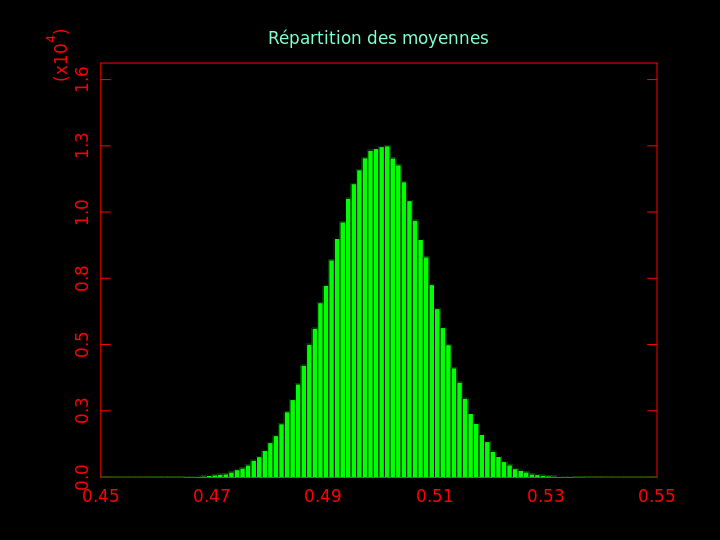
Activité 9
Une autre caractéristique importante (qui saute aux yeux dans le cas d'une distribution normale) est l'étalement de la distribution des valeurs autour de la moyenne. Celle-ci est mesurée par l'écart-type.
L'écart-type est la racine carrée de la variance. Celle-ci se définit très simplement comme la moyenne de l'écart au carré entre chaque échantillon et la moyenne empirique : \( var (x_i) = \frac{1}{n} \sum_{i=1}^{i=n} (x_i - \hat{\mu})^2 \).
Pour ce qui est de l'écart-type, il en existe deux versions : une version biaisée et une version non biaisée. Si on prend la racine carrée de la variance, on obtient l'écart-type biaisé. Biaisé signifie qu'en moyenne, sa valeur diffère du vrai écart-type \( \sigma \). L'écart-type non biaisé (noté \( \widehat{\sigma_c} \) avec un 'c' en indice pour indiquer qu'il est corrigé) est obtenu en divisant non pas par n mais par n-1 : $$ \widehat{\sigma_c} = \sqrt{\frac{1}{n-1} \sum_{i=1}^{i=n} (x_i - \hat{\mu})^2} $$
| C | python |
|---|---|
|
La fonction |
Toujours prompt à ne pas bien faire les choses, la fonction |
Question 9 : écrire un programme qui génère 100000 nombres pseudo-aléatoires tirés selon une loi normale \( {\cal N} (\mu, \sigma) \) pour des valeurs de \( \mu \) et \( \sigma \) que vous fixez à votre goût. Calculer les deux écarts-types et comparez-les entre-eux et avec la vraie valeur de l'écart-type.
Activité 10
Une autre manière de mesurer l'étalement d'une distribution de nombres consiste à déterminer la proportion d'échantillons qui sont à une certaine distance d de la moyenne \( \mu \) soit dans l'intervalle \( [ \mu - d; \mu + d ] \).
Question 10 : écrire une fonction qui prend en paramètre un tableau de nombres pseudo-aléatoires, une valeur de a et une valeur de b et qui renvoie la proportion d'éléments du tableau dont la valeur est comprise entre a et b.
Question 10bis : utilisez la fonction précédente pour déterminer la proportion de nombres qui se situent à 1 écart-type de la moyenne, puis 2 écarts-types de la moyenne, puis 3 écarts-types de la moyenne. Appliquez-la à 100000 nombres pseudo-aléatoires tirés selon une loi \( {\cal N} (\mu, \sigma) \) dont vous fixez les paramètres comme vous l'entendez.
La théorie nous dit que 68% des échantillons sont à moins d'un écart-type de la moyenne, 95% à moins de 2 écarts-types, 99,7% à moins de 3 écarts-types. Retrouvez-vous ces proportions ?
Activité 11
Une dernière notion que nous définissons est celle de quantile : α étant un nombre réel quelconque, le quantile α d'un ensemble d'échantillons est la proportion de ces échantillons dont la valeur est < α.
Question 11 : écrire une fonction qui prend en paramètre un tableau de nombres et la valeur de \( \alpha \) et renvoie le quantile α des éléments de ce tableau.
Question 11bis : utilisez la fonction précédente pour déterminer le quantile α d'un ensemble de 100000 nombres pseudo-aléatoires tirés selon une loi \( {\cal N} (0, 1) \) pour chaque valeur de α variant de -5 à 5 par pas de 0,1. Faites-une représentation graphique de ces quantiles.
Question 11ter : comment utilisez-vous cette fonction pour déterminer la valeur empirique de la médiane du tableau de nombres ?
Activités libres
On indique ici des activités supplémentaires. Vous êtes vivement encouragés à les réaliser.
- la notion statistique d'estimation est présentée de manière intuitive dans l'annexe C du polycopié de cours.
Processus de Markov
Dans cette partie du TP, on s'intéresse à des processus de markov. Un processus de markov est un processus dynamique (qui se déroule au cours du temps) en temps discret, caractérisé par un état courant \( x_t \) (à l'instant t) et tel que l'état suivant (à l'instant t+1) ne dépend que de l'état courant et, en général, d'un aléa. S'il n'y a pas d'aléa, le processus est déterministe ; il est stochastique sinon. \( x_0 \) est son état initial. Une fonction de transition définit \( x_{t+1} \) en fonction de \( x_t \).
Activité 12
On considère un processus de markov défini par :
$$ x_{t+1} = \left\{ \begin{eqnarray*} x_t - 1 \mbox{ avec probabilité } \frac{1}{2} \\ x_t + 1 \mbox{ avec probabilité } \frac{1}{2} \end{eqnarray*} \right. $$
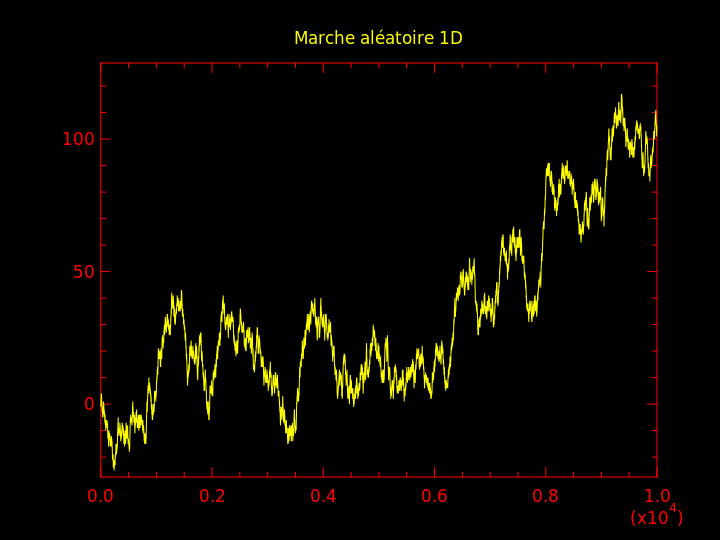
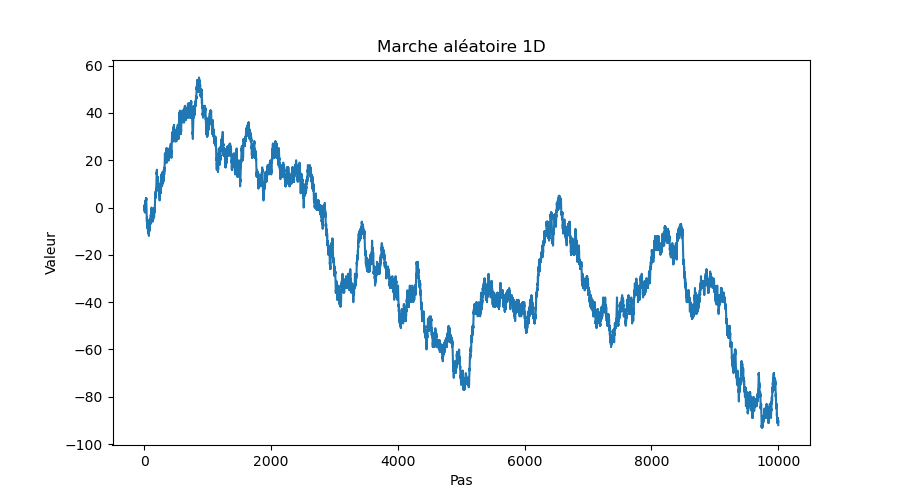
Question 12 : en prenant \( x_0 = 0 \), simuler ce processus pendant \( 10^4 \) pas de temps et réaliser un graphique indiquant l'état en fonction du temps.
| C | python |
|---|---|
|
Pour la partie graphique, on utilisera la fonction |
En python, on utilise la fonction |
On obtient une marche aléatoire. Seul l'aléa guide l'évolution de l'état. Quoique totalement aléatoire, on note que la séquence d'états possède certaines caractéristiques frappantes : lesquelles ?
Question 12bis : en prenant \( x_0 = 0 \), réaliser 5 marches aléatoires, chacune étant obtenu en ré-initialisant le processus en \( x_0 = 0 \) au bout de \( 10^4 \) pas. En faire un graphique.
Même question que la précédente mais en même temps que l'on ré-initialise \( x_0 \), ré-initialiser la graine du générateur de nombres pseudo-aléatoires. (Conservez bien l'ensemble des graines que vous utilisez et l'ordre dans lequel vous les utilisez.)
Comparer les 2 graphiques obtenus.
J'obtiens respectivement pour ces deux questions :
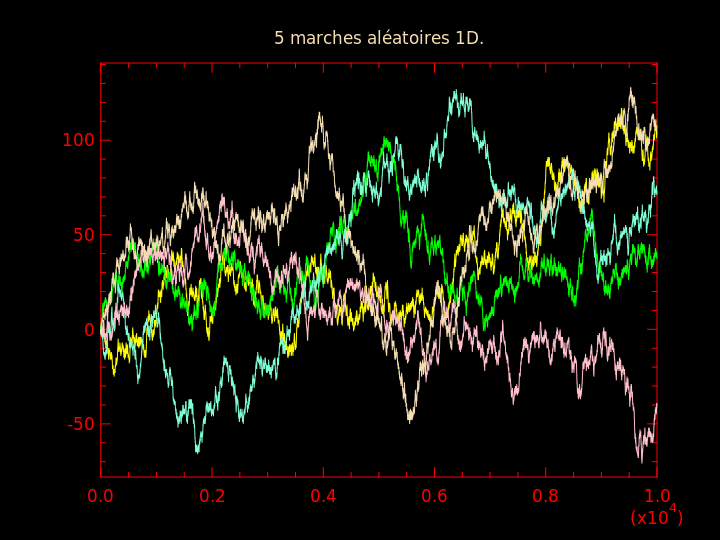
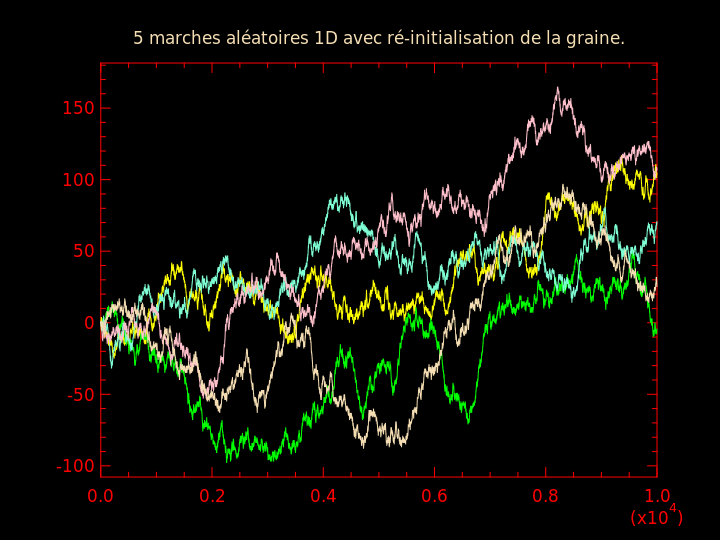
Activité 13
On va réaliser le même genre de chose dans le plan : un point bouge de manière aléatoire à chaque pas de temps.
$$ \left\{
\begin{eqnarray*}
x_{t+1} \gets x_t + c {\cal N} (0, 1) \\
y_{t+1} \gets y_t + c {\cal N} (0, 1)
\end{eqnarray*}
\right.
$$
\( c \) est un facteur que je vous laisse choisir pour que la figure soit jolie. Par abus de notation, je note \( {\cal N} (0, 1) \) un nombre pseudo-aléatoire tiré selon une loi normale centrée réduite.
Question 13 : en prenant \( x_0 = y_0 = 0 \), simuler ce processus pendant \( 10^4 \) pas de temps et réaliser un graphique des \( (x_t, y_t) \) au fil du temps.
| C | python |
|---|---|
|
On utilise la fonction
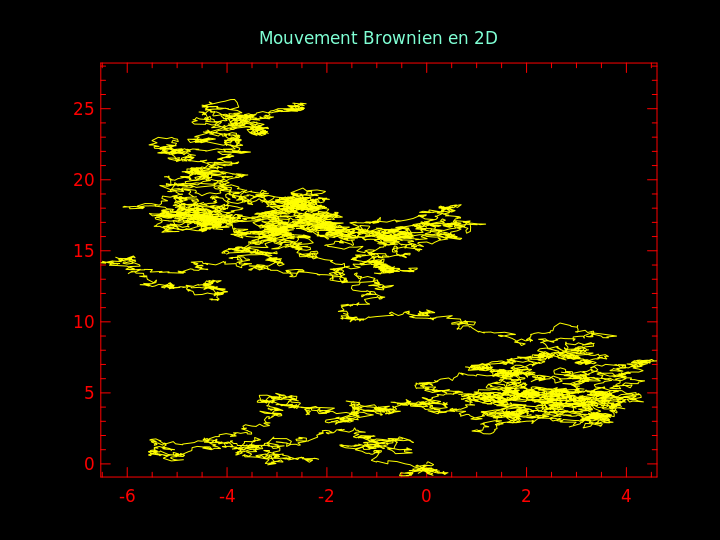
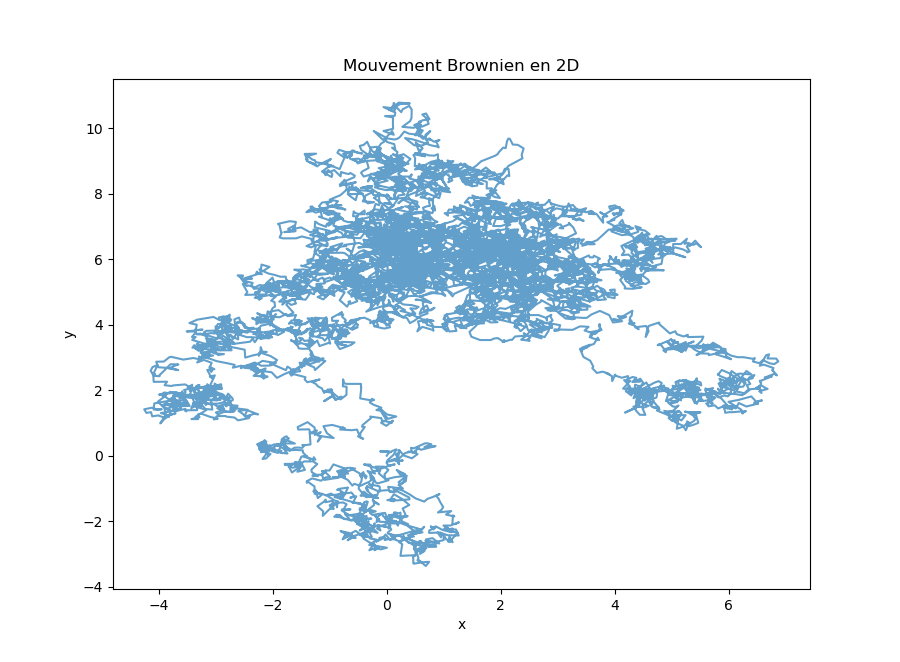
J'obtiens ce graphique :
|
En python, on utilise la fonction |
Ce graphique illustre le déplacement aléatoire d'une particule et porte le nom de « mouvement brownien » lorsque la variation des coordonnées suit une loi normale. La particule peut se mouvoir dans un espace de dimension quelconque, pas forcément dans le plan.
Activité 14
On peut aussi marcher dans un graphe. Par exemple, prenons le graphe ci-dessous :
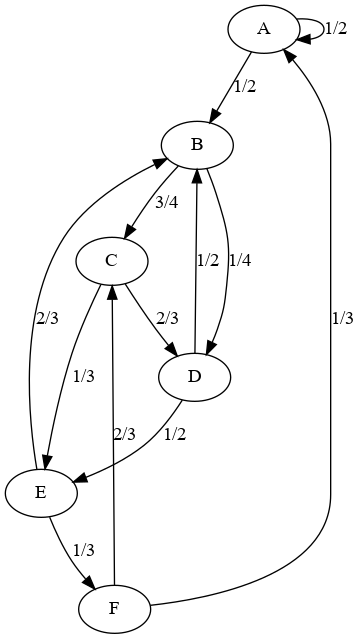
Chaque arête est orientée et est étiquetée avec la probabilité de la suivre. Par exemple, dans le nœud A, on a une chance sur deux de rester dans A ou d'aller vers le nœud B ; de même, dans le nœud C, on a deux chances sur 3 d'aller en D, une chance sur 3 d'aller en E.
Question 14 : on part du nœud 0 et on effectue un certain nombre de transitions. Cela va entraîner une marche aléatoire dans le graphe. On s'intéresse à estimer la probabilité d'occupation de chaque nœud. Pour cela, on va simplement effectuer un grand nombre de transitions aléatoires dans le graphe, compter le nombre de visites à chacun des nœuds et finalement, diviser ce nombre par le nombre de pas réalisés. Vous faites cela un certain nombre de fois (100 par exemple) et pour obtenir la moyenne et l'écart-type de ces probabilités d'occupation. Vous les affichez.
Question 14bis : est-ce que le résultat change si on part d'un autre état initial ?
Question 14ter : mêmes questions pour ce graphe :
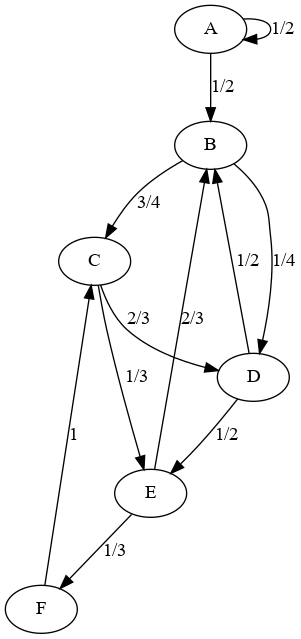
Qu'observez-vous ? Expliquez.