Laissez-moi sortir !

Vous allez réaliser une expérience. Celle-ci consiste à trouver la sortie d'un labyrinthe. Contrairement aux labyrinthes que vous survolez, vous allez être immergé dans le labyrinthe (enfin presque).
Le but est de mesurer votre courbe d'apprentissage face à cette tâche : allez-vous trouver la sortie de plus en plus vite ?

Dans R, tapez la commande source ("https://philippe-preux.github.io/ensg/aeac/tps/labyrinthe/laby.R")
(Faites un copier/coller pour éviter les fautes de frappes.)
L'expérience est lancée ; passez-là.
Un graphique apparaît ressemblant à celui-ci (ce n'est pas exactement celui-là, c'est normal) :

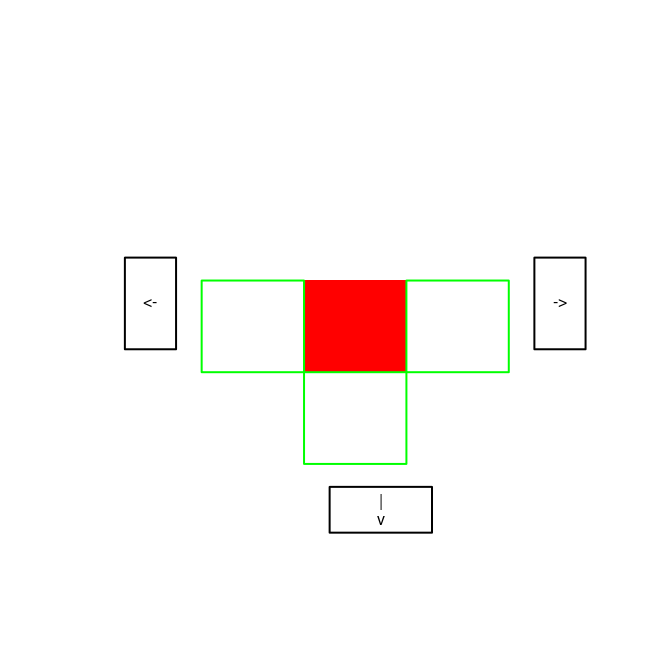
Vous vous trouvez dans la case rouge et vous pouvez vous déplacer dans l'une des cases bordées de vert en cliquant dans l'une des cases de direction.
Quand vous serez à côté de la sortie, vous verrez ceci :

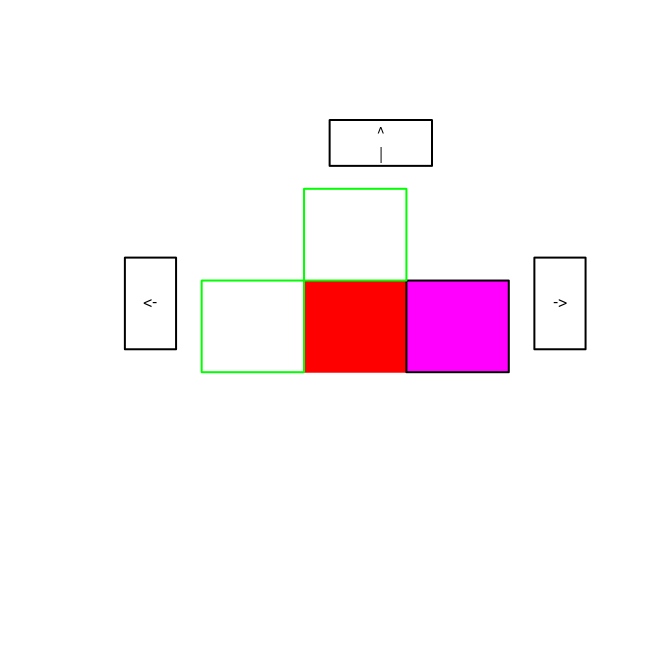
Vous êtes dans la case rouge et la sortie et en magenta. Il vous reste 1 pas à faire dans la bonne direction. Faites-le.
Vous aurez alors la fenêtre suivante :

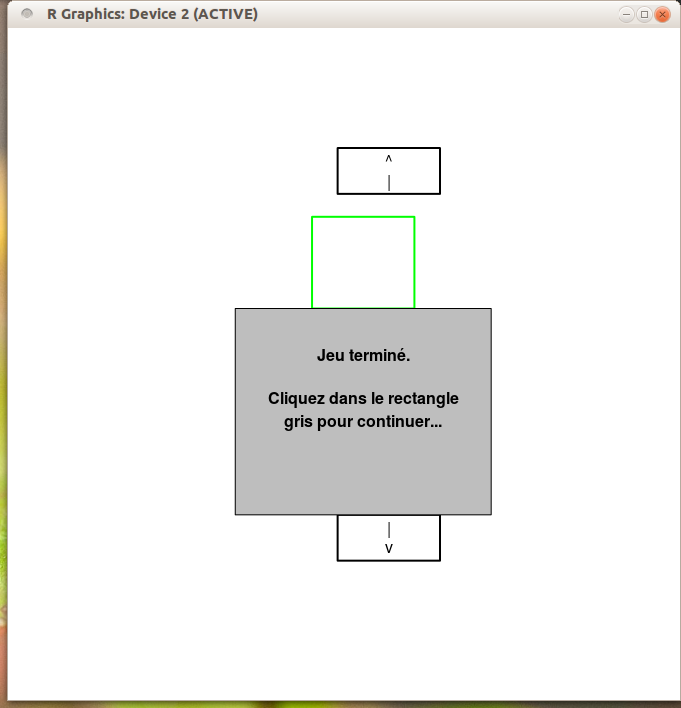
Cliquez dans le rectangle gris comme demandé et on recommence.
Vous le refaites 20 fois.

Fichier de résultats

Le fichier laby4....txt contient une ligne par clic. Chaque ligne contient les informations suivantes :

le numéro de l'épisode (entre 1 et 20)
le numéro du clic/mouvement durant l'épisode
l'instant du clic
le nombre de secondes écoulées depuis le début de l'épisode
le numéro de la case dans laquelle on se trouve (un nombre entier)
le mouvement effectué (gauche = 1, droite = 2, haut = 3, bas = 4)
1 si la sortie est atteinte, 0 sinon
1 si l'épisode est terminé, 0 sinon

Analyse des résultats expérimentaux

Tous les éléments pour résoudre ces questions ont été vus précédemment.

Chargez le fichier de résultats dans un data.frame dénommé resultats. Les colonnes seront nommées respectivement : episode, clic, instant, t, n, mvt, sortie, fin.
Remarque : un épisode s'arrête soit parce que la sortie a été atteinte, soit parce que vous avez effectué 200 clics sans trouver la sortie. Quelle qu'en soit la raison, l'attribut fin indique si l'épisode est fini ou pas.
Sur les 20 épisodes, combien de fois avez-vous atteint la sortie ?
Lors de quels épisodes n'avez-vous pas atteint la sortie ?
Mettez dans un vecteur dénommé nb.clics.pour.sortir ce nombre de clics que vous avez effectués pour atteindre la sortie. Si la sortie n'a pas été atteinte, mettez NA.
En moyenne, en combien de clics avez-vous atteint la sortie ?
Faites un graphique de ce nombre de clics pour sortir pour chaque épisode (l'épisode en abscisses, le nombre de clics en ordonnées ; si NA, ne mettez-rien).
Observez-vous une tendance ? Ce nombre de clics pour atteindre la sortie semble-t-il diminuer au fil des épisodes ?
Ajoutez à votre graphique une ligne horizontale indiquant la moyenne et ajoutez une ligne en pointillés à - 1 écart-type et + 1 écart-type.
Ajoutez-y aussi une ligne un peu plus épaisse qui représente la médiane.

Durée des épisodes :

Mettez dans un vecteur dénommé duree.des.episodes le temps (en secondes) qu'a duré chacun des épisodes.
Y a-t-il une corrélation linéaire entre la durée d'un épisode et le nombre de clics pendant l'épisode ?
Faites un plot de la durée d'un épisode en fonction du nombre de clics pendant l'épisode. Cela confirme-t-il votre réponse à la question précédente ?
Pour cette question et la suivante, on ne s'intéresse qu'aux épisodes au cours desquels vous avez atteint la sortie. Mettez dans un vecteur dénommé duree.episodes.ayant.atteint.la.sortie la durée de l'épisode.
Cette durée a-t-elle tendance à diminuer ?

Temps d'émission d'un comportement :

Mettre dans un vecteur dénommé tec (tec pour « Temps d'Émission d'un Comportement ») le temps d'émission de chacun des comportements que vous avez émis.
Quel est le temps moyen d'émission d'un comportement ? Son écart-type ?
Faites un histogramme de ces temps (utiliser la commande hist en faisant un nombre suffisant de paquets pour voir quelque chose).
Cet histogramme a-t-il une forme caractéristique ? La distribution semble-t-elle normale ? ...
Les valeurs composant l'histogramme peuvent être mises dans un objet pour pouvoir ensuite les manipuler.
Ainsi, précédemment, vous avez tapé quelque chose comme :
```
hist (tec)
```
Vous pouvez aussi taper :
```
tec.hist <- hist (tec)
```
qui met dans l'objet tec.hist un ensemble d'informations, parmi lesquelles :
- tec.hist$breaks contient la valeur minimale de chaque intervalle
- tec.hist$mids contient la valeur au milieu de chaque intervalle
- tec.hist$counts contient le nombre de valeurs situées dans cet intervalle
- tec.hist$density contient la proportion de valeurs situées dans cet intervalle (autrement dit, tec.hist$counts / length (tec)).
(notez la notation avec un $ ; breaks, mids, ... se nomment des attributs de l'objet tec.hist).
Si vous faites :
```
  plot (tec.hist$mids, tec.hist$counts)
```
vous retrouvez l'histogramme (encore mieux si vous ajoutez type = "h" dans le plot).
Faites un plot du logarithme de l'attribut counts en fonction du logarithme de l'attribut mids.
Vraisemblablement, la plupart des points sont maintenant alignés.
Une distribution de valeurs qui a cette allure est dite en loi de puissance (du moins, si on veut parler plus précisèment, on peut suspecter une loi de puissance ; il faudrait faire des tests statistiques pour s'en assurer avec une certaine confiance).
Calculer le coefficient de corrélation linéaire entre les logarithmes de ces deux attributs. Conclure. (Attention, le log de 0 est moins l'infini : il faut éliminer ces valeurs pour pouvoir calculer la corrélation avec cor()).

Déterminer s'il y a des actions qui prennent significativement plus de temps à être émises que les autres. Ces actions sont-elles particulières ? Sont-elles émises dans des zones particulières du labyrinthe ? Durant la tâche ? Durant certains épisodes ? ...
Pour vous aider, je vous dévoile le plan du labyrinthe.

Divers :

Créer une matrice dénommée décomptes.des.mvt ayant le nombre de lignes et de colonnes adéquat pour répondre à la question qui suit. Dans cette matrice, vous mettez le nombre de clics sur chacun des mouvements pour chacun des épisodes. Autrement dit, la ligne i de la matrice contient le nombre de mouvements 1 (à gauche) dans la colonne 1, ... le nombre de mouvements 4 (vers le bas) dans la colonne 4.
Créer une matrice dénommée nb.visites ayant autant de lignes que d'épisodes et autant de colonnes que de cases. Remplissez-la avec le nombre de visites à une case donnée lors de chacun des épisodes.

Pour chaque épisode, déterminez le nombre de cases que vous avez visitées durant l'épisode. Mettez cette information dans un vecteur dénommé nb.cases.visitées
Faites un plot des valeurs de ce vecteur.
Observez-vous une tendance ?

Le vecteur distance.a.la.sortie contient le nombre de clics à effectuer pour atteindre la sortie par le chemin le plus court à partir d'une case spécifiée par son numéro. Faites un plot représentant cette distance à chaque clic de chaque épisode.
Faites le plot représentant la distance en fonction du temps écoulé depuis le début de l'épisode.
Pour chaque épisode, comptez le nombre de clics qui vous ont éloigné de la sortie. Mettez ces décomptes dans un vecteur dénommé nb.clics.qui.eloignent.
Faites un plot des valeurs de ce vecteur.
Observez-vous une tendance ?
Ce nombre de clics qui éloignent est-il corrélé au nombre de clics effectués durant chacun des épisodes ?
Pour chaque épisode, déterminez la proportion d'actions qui ont été optimales (c'est-à-dire, les actions vous ont rapproché de la sortie). Mettez ces proportions dans un vecteur dénommé proportion.actions.optimales
Faites un plot des valeurs de ce vecteur.
Observez-vous une tendance ?