Le problème d'assignement du crédit

Face à une bande de bandits

Vous allez réaliser une expérience de bandits à 4 bras. Pour cela : lancer R (si vous ne savez plus comment on fait, cliquez ici). Dans R, tapez la commande source ("https://philippe-preux.github.io/ensg/aeac/tps/bandits/4bras.Steyvers-et-al.R") (Faites un copier/coller pour éviter les fautes de frappes.) L'expérience est lancée ; passez-là.

Étude de vos données expérimentales

Chargement des données et quelques graphiques simples

Durant l'expérience, un certain nombre d'informations ont été enregistrées à chaque clic. Elles sont dans le fichier dénommé 4bS.res.xxx.yyy.txt où xxx et yyy vous identifie ainsi que votre machine. Cette identification a pour seul but de pouvoir différencier les fichiers les uns des autres.

Pour les manipulations ci-dessous, celles que nous avons déjà rencontrées ne sont pas expliquées. Si vous avez oublié comment faire, allez consulter le TP de découverte de R.

• On va charger ce fichier dans R à l'aide de la fonction read.table(). Afin de rendre les manipulations qui vont suivre plus simples, on donne un nom aux attributs qui correspondent aux colonnes du fichier. Aussi, vous taperez une commande du genre :

  > donnees <- read.table ("4bS.res.xxx.yyy.txt", 
       col.names = c ("jeu", "essai", "epoque", "delta.t", "choix", "s", "r", "r.cumule",
                      "p1", "p2", "p3", "p4"))
  

  Bien entendu, vous mettez le nom de fichier correct.
• On peut jeter un coup d'œil aux premières données en tapant head (donnees).
  La première ligne indique le nom des attributs/colonnes et en dessous sont indiquées les 6 premières données.
  Quand on donne un nom aux attributs, on peut ensuite accéder à la valeur d'un attribut soit en spécifiant son numéro de colonne (cf. TP de découverte), soit en spécifiant son nom :
  • donnees [1, 7] et donnees$r [1] spécifient la même information : la valeur de l'attribut r de la 1^ère donnée. L'attribut r est en 7^è colonne.
  L'époque indique l'instant du clic : c'est un nombre de secondes. Ce qui compte ici est l'écart entre deux lignes successives ; c'est le temps qui s'est écoulé entre deux clics. Ce temps écoulé entre un clic et le suivant est dans la colonne 4, attribut dénommé delta.t.


• Faites un graphique représentant ce temps écoulé entre deux clics. Constatez-vous quelque chose ?
• Il est possible que vous voyiez des points anormaux. Si c'est le cas, analysez-les pour comprendre leur origine.
• Utilisez la fonction cor() pour calculer la corrélation entre cet intervalle de temps entre deux clics et le retour obtenu. Ces deux attributs sont-ils corrélés (linéairement) pour vous ?


• Faites un graphique de l'attribut r.cumule. Constatez-vous quelque chose ?
• Faites un graphique de l'attribut r.cumule en fonction de l'attribut epoque. Constatez-vous quelque chose ?
• Dans ce graphique, faites en sorte que le nombre de secondes depuis le début de l'expérience soit affiché sur l'axe des x. Constatez-vous quelque chose ?
• Faites un graphique de l'attribut r.cumule en fonction de l'attribut delta.t. Constatez-vous quelque chose ?
• Faites un graphique de l'attribut r.cumule en fonction de l'attribut jeu. Constatez-vous quelque chose ?

Sélection d'éléments dans un data.frame

On peut facilement sélectionner des données répondant à un certain critère. Ainsi :

• si l'on veut uniquement les données du jeu numéro 4, on tapera la commande donnees [donnees$jeu == 4,].
• Si l'on veut les données des jeux 4 à 7 : donnees [donnees$jeu %in% (4:7),].

Notez bien la virgule avant le crochet fermant ,] qui reprend la syntaxe vue la fois précédente  [ ligne(s), colonne(s) ].
Notez bien également l'opérateur == pour tester l'égalité entre deux objets. De même, on a != pour différent, <, <=, > et >=.

• Affichez le nombre de retours cumulés obtenus à l'issue de chaque jeu (autrement dit, à chaque fois que l'attribut essai est égal à 20).
• Mettez-le dans une variable dénommée retours.cumules.finaux
• Faites-en un plot. Voyez-vous une tendance ?
• Faites-en un histogramme en utilisant la fonction hist().
• Pour chaque choix, comptez le nombre de succès obtenus sur l'ensemble des jeux. L'attribut choix vaut 1, 2, 3 ou 4, selon l'endroit où vous avez cliqué.

On peut combiner plusieurs conditions. Ainsi, pour sélectionner les données du jeu numéro 2 pour lesquels il y a eu un succès, on tapera :

> donnees [(donnees$jeu == 2) & (donnees$r == 1),]

L'opérateur & dénote le et-logique. Notez les parenthèses autour de chaque condition.

• Pour chaque choix, comptez le nombre de succès obtenus durant le jeu 1. L'attribut choix vaut 1, 2, 3 ou 4, selon l'endroit où vous avez cliqué.
• Même question sur le jeu 20.
• Même question sur le jeu 1 à 5, 6 à 10, 11 à 15 et 16 à 20.
• Durant quel jeu avez-vous obtenu un score (r.cumule) maximum/minium ?
• Quel est ce score ?

Rappelez-vous qu'existent les fonctions min () et max (). Sachez aussi qu'il existe les fonctions which.min () et which.max ().

Répéter plusieurs fois le même traitement : la boucle

Introduction à la notion de boucle

Si on veut avoir les décomptes des succès pour chaque choix pour chaque jeu, on va devoir taper beaucoup de choses. On peut faire beaucoup plus simple en utilisant une boucle ; pour commencer, tapez ce qui suit :

> for (i in 1:10) {
    print (i)
  }

vous obtenez l'affichage des nombres de 1 à 10. Expliquons ce qui vient de se passer :

• for (i in 1:10) signifie : pour les valeurs de la variable i variant de 1 à 10 : c'est-à-dire, i va successivement prendre les valeurs 1, 2, 3, ... jusque 10.
• effectuer pour chacune de ces valeurs les instructions qui se trouvent entre les { }
• ici, il y a une instruction qui affiche la valeur de i. On aurait pu effectuer d'autres traitements plus intéressants.

Le nombre de clics sur un choix est-il corrélé à la probabilité de succès associée à ce choix ?

Avec cette notion de boucle, vous pouvez maintenant afficher le nombre de clics sur chaque choix à chaque jeu.
Pour manipuler aisément ces décomptes, il faut les placer dans une matrice. Cette matrice stockera pour chaque jeu et chaque choix le nombre de clics. Cette matrice a donc 20 lignes (une par jeu) et 4 colonnes (une par choix). Pour créer cette matrice, on tapera :

> decomptes.tirages <- matrix (nrow = 20, ncol= 4)

Les éléments d'une matrice sont accédés comme ceux d'un data.frame, par la notation [ ligne, colonne ].
On peut aussi affecter tous les éléments d'une colonne à la fois : par exemple, decomptes.tirages [2, ] <- c (2, 8, 3, 1) affecte tous les éléments de la 2^è ligne de la matrice.
On veut étudier la question suivante : a-t-on tendance à cliquer de plus en plus, voire exclusivement, sur le meilleur choix au fil des essais d'un jeu ? On a envie que la réponse à cette question soit plutôt positive.
Faisons un graphique des décomptes calculés ci-dessus. Cela donne quelque chose ressemblant à la figure de gauche ci-dessous. Faites cette figure avant de continuer.
Les fonctions which() et length() peuvent être utiles...

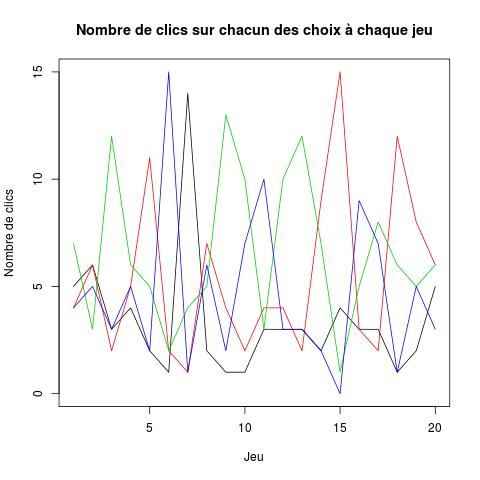
On ne voit pas grand chose sur ce graphique. Le fait qu'à chaque jeu, la probabilité de succès de chaque choix change fait que représenter le nombre de clics sur chaque choix n'éclaire pas la question que nous nous posons.
Pour que la figure soit informative, il faudrait que le choix 1 soit toujours le plus mauvais, ... le choix 4 toujours le meilleur. Si l'expérience n'a pas été menée ainsi pour des raisons évidentes, rien ne nous empêche de re-numéroter les choix à chaque jeu pour que les choix soient numérotées de cette manière. Comment faire ?
La fonction sort() effectue un tri. Par exemple, vous pouvez taper :

> sort (c (.2, .3, .05, .45))

et vous obtenez :

[1] 0.05 0.20 0.30 0.45

Vous pouvez aussi taper :

> sort (c (.2, .3, .05, .45), index.return = TRUE)

et vous obtenez :

$x
[1] 0.05 0.20 0.30 0.45

$ix
[1] 3 1 2 4

Cette notation indique que le résultat est un objet ayant deux attributs :

• l'attribut x qui est un vecteur des nombres triés ;
• l'attribut ix qui est un vecteur indiquant l'indice d'origine de chaque nombre, avant le tri : 0,05 était en 3^è position avant le tri, 0,2 en 1^ère, ...

Si vous mettez le résultat dans un objet comme suit :

> resultat.du.tri <- sort (c (.2, .3, .05, .45), index.return = TRUE)

vous pouvez ensuite accéder à ces deux informations par resultat.du.tri$x et resultat.du.tri$ix.
Supposons maintenant que nous ayons deux objets :

• une liste de valeurs valeurs.associees <- c (12, 15, 8, 13)
• la liste de valeur précédentes valeurs.de.tri <- c (.2, .3, .05, .45))

On peut imaginer que les secondes sont des probabilités de succès sur chacun des 4 choix et que les premières sont les nombres de clics sur chaque choix. Ainsi, les premières sont associées aux secondes : 12 est associé à la probabilité 0,2, 15 à la probabilité 0,3, ... Si on trie les probabilités par ordre croissant, pour obtenir les valeurs associés à chaque probabilité, il faut les ré-ordonner également. Cela s'obtient comme suit :

> resultat.du.tri <- sort (c (.2, .3, .05, .45), index.return = TRUE)
> resultat.du.tri$x
[1] 0.05 0.20 0.30 0.45
> valeurs.associees [resultat.du.tri$ix]
[1]  8 12  15 13

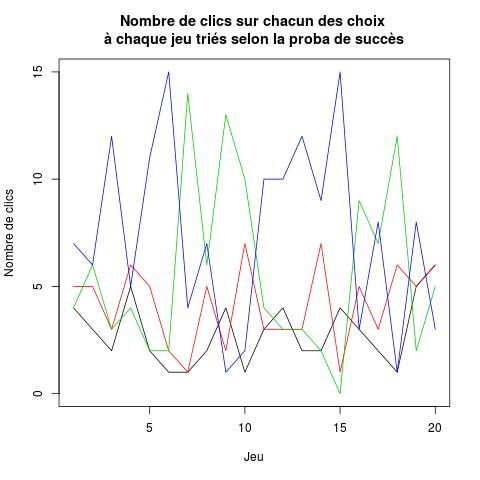
Vous allez maintenant vous inspirer de cela pour réaliser un graphique comme celui de droite ci-dessus qui représente le nombre de clics sur chaque choix ; cette fois-ci, ceux-ci sont renumérotés en fonction de leur probabilité de succès (1 = le choix dont la probabilité de succès est la plus faible, ... 4 = le choix dont la probabilité de succès est la plus forte). Les couleurs sont affectées comme suit : noir pour le choix 1, rouge pour le choix 2, vert pour le choix 3, bleu pour le choix 4. Les numéros de ces couleurs sont 1, 2, 3, 4 respectivement (les choses sont bien faites...).

Les probabilités sont ici stockées dans le data.frame donnees, dans les attributs p1 à p4, soit les attributs 9 à 12. On peut obtenir ces probabilités par donnees [1, 9:12] pour le 1^er jeu. Cela est lui-même un data.frame. Si on veut trier ces valeurs, il faut les mettre dans un vecteur. Cela se fait à l'aide de la fonction as.numeric : as.numeric (donnees [i, 9:12]).

En préalable à la réalisation du graphique, vous stockerez ces décomptes dans une matrice dont la colonne i ne contiendra plus le nombre de clics sur le choix i, mais le nombre de clics sur le choix dont la probabilité est la i^è quand celles-ci sont ordonnées dans l'ordre croissant. Dans la suite, on nommera cette matrice decomptes.tirages.tries.

Pour cela, on va partir de la matrice decomptes.tirages et, pour chaque ligne, on va trier les colonnes en fonction des probabilités de succès.
Si on considère la 1^ière ligne, il faut donc trier decomtes.tirages [,1] en fonction des probabilités de succès. Ces probabilités de succès sont constantes durant tout le 1^ier jeu ; on les trouve dans donnees [1,9:12] par exemple (mais aussi dans donnees [2,9:12], donnees [3,9:12], ... donnees [20,9:12]).
Il s'agît donc de trier ces probabilités et d'utiliser leur ordre pour ré-ordonner les éléments de la première ligne de la matrice :

tri <- sort (as.numeric (donnees [1, 9:12]), index.return = TRUE)
decomptes.tirages.tries [1, ] <- decomptes.tirages [1, tri$ix]

Pour les 19 lignes suivantes, c'est la même chose ; on peut donc mettre cela dans une boucle.
La petite difficulté restante est de trouver les probabilités associées à chaque jeu. Pour le jeu 1, l'une parmi les 20 premières lignes de donnees les contient (cf. ci-dessus). Pour le jeu 2, ces probabilités sont dans donnees [21,9:12], donnees [22,9:12], donnees [23,9:12], ... donnees [40,9:12]. Pour le jeu 3, ces probabilités sont dans donnees [41,9:12], donnees [42,9:12], donnees [43,9:12], ... donnees [60,9:12]... Pour le jeu 20, ces probabilités sont dans donnees [381,9:12], donnees [382,9:12], donnees [383,9:12], ... donnees [400,9:12].
On remarque que pour le jeu j, ces probabilités sont dans donnees [20 * j,9:12].

Quand on met tout cela bout à bout, on obtient ce qui suit :

decomptes.tirages.tries <- decomptes.tirages
for (j in 1:20) {
  tri <- sort (as.numeric (donnees [j * 20, 9:12]), index.return = T)
  decomptes.tirages.tries [j, ] <- decomptes.tirages.tries [j, tri$ix]
}

À l'issue de l'exécution de cette boucle, la variable decomptes.tirages.tries contient les valeurs attendues dans les différentes colonnes : la colonne 1 correspond au choix dont la probabilité de succès est la plus faible, ainsi de suite jusque la colonne 4 qui contient le nombre de clics sur le choix ayant la plus grande probabilité de succès.

• Une fois le graphique réalisé, constatez-vous quelque chose ?
• Y a-t-il un lien entre le nombre de clics sur le i^è choix trié et i ? Vous pouvez calculer la proportion de clics sur chacun des choix pendant chacun des jeux. Conclusion ?

Autres activités avec des boucles

• Mettez dans une matrice le nombre de succès obtenus à chaque jeu pour chaque choix ;
• pour chaque jeu, déterminez le choix ayant obtenu le plus grand nombre de succès.

• Produire un graphique comme celui-ci :
  
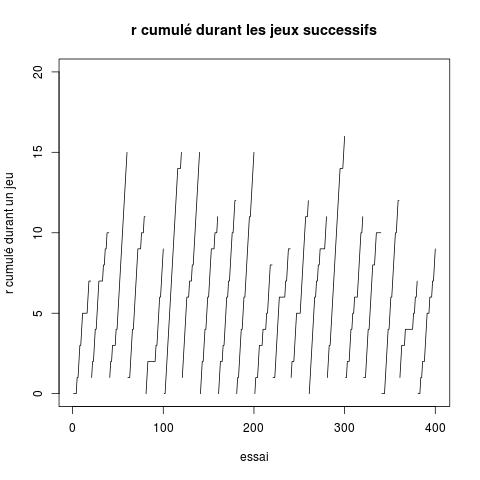
  qui représente l'attribut r.cumulé au fil des essais et des jeux.

Étude des comportements émis

On pose quelques questions plus ouvertes pour analyser le comportement que vous avez émis. Pour y répondre, il faut réflêchir à une méthode et la mettre en œuvre.

Scores maximal et moyen

• Quel est le score maximal moyen que l'on peut obtenir à chaque jeu ? (précision : c'est le score maximal moyen, c'est-à-dire : imaginons que l'on répète plusieurs fois un même jeu, donc avec un même ensemble de probabilités de succès associé aux 4 choix. Le score maximal moyen est la moyenne des retours cumulés obtenus lors de cette répétition.
• À chaque jeu, quel est le score moyen si on a un comportement aléatoire (choix uniforme) ?
• Où se situent vos scores ?
• Faites le graphique suivant (qui reprend le précédent et le complète) :
  
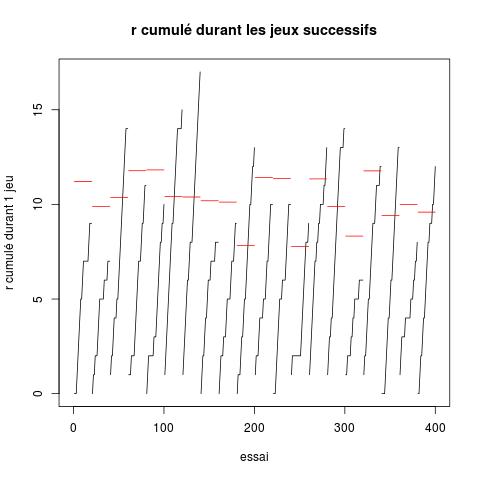
  Sur ce graphique, pour chaque jeu, on indique la performance moyenne espérée si on fait les choix selon un tirage aléatoire uniforme.

Relation entre nombre de clics et probabilité de succès

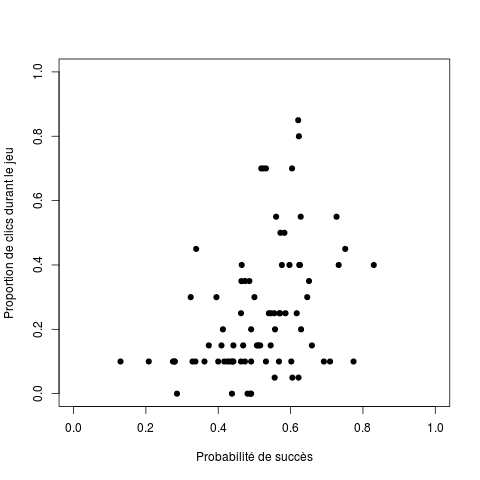
A-t-on cliqué plus souvent sur les choix dont la probabilité de succès est élevée ?
Pour le savoir, faire un graphique indiquant en abscisses la probabilité des choix et en ordonnées, le nombre de clics sur ce choix. On obtiendra un graphique dans ce genre-là :

Variabilité du comportement intra-jeu

On se demande si le comportement est plus varié au début d'un jeu qu'à la fin. Cette variabilité est-elle plus faible à la fin d'un jeu ? ...

• Comment étudiez-vous cette question ?
• Quelle est votre conclusion concernant votre comportement ?